АМАНИПУЛИРОВАНИЕ РЕЛЯЦИОННЫМИ ДАННЫМИ
Манипулятивная часть реляционной модели состоит из множества операций, получивших в совокупности название реляционной алгебры, и реляционной операции присваивания, которая присваивает значение некоторого произвольного выражения этой алгебры другому отношению. Обсудим сначала реляционную алгебру.
Каждая операция реляционной алгебры использует одно или два отношения в качестве ее операндов и продуцирует в результате некоторое новое отношение. Первоначально Кодд определил восемь таких операций, две группы по четыре операции в каждой: 1) традиционные теоретико-множественные операции объединения, пересечения, разности и декартова произведения, которые были несколько модифицированы с тем, чтобы принять во внимание тот факт, что их операнды являются отношениями, а не произвольными множествами и 2) специальные реляционные операции селекции, проекции, соединения и деления. Эти восемь операций символически показаны на рис. А.2. Ниже дается краткое определение каждой из них. Для простоты в этих определениях предполагается, что в отношениях принимается упорядочение атрибутов слева направо — не потому, что это необходимо сделать, а для того, чтобы упростить обсуждение.
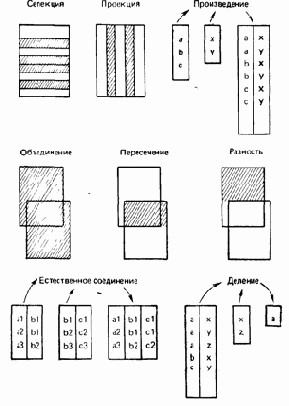
Риc. A.2.
Реляционная алгебра
Традиционные теоретико-множественные операции
В каждой из традиционных теоретико-множественных операций используются два операнда. Для всех операций, кроме декартова произведения, эти два операнда должны быть совместимыми по объединению, т. е. они должны быть одной и той же степени, например п, и i-e их атрибуты (i = 1, 2, ...,. п) должны быть связаны с одним и тем же доменом. Они не должны, однако, иметь одинаковое имя.
— Объединение
Объединением двух (совместимых по объединению) отношений А и В называется множество всех кортежей t, принадлежащих либо А, либо В, либо им обоим.
Пример в языке SQL:
SELECT НОМЕР_ПОСТАВЩИКА FROM S
UNION
SELECT НОМЕР_ПОСТАВЩИКА FROM SP;
— Пересечение
Пересечением двух (совместимых по объединению) отношений А и В называется множество всех кортежей t, каждый из которых принадлежит как А, так и В.
Пример в языке SQL;
SELECT НОМЕР_ПОСТАВЩИКА FROM S
WHERE EXISTS
(SELECT НОМЕР_ПОСТАВЩИКА FROM SP
WHERE SP.HOMEP_ПОСТАВЩИКА =
S.НОМЕР_ПОСТАВЩИКА);
— Разность
Разностью между двумя (совместимыми по объединению) отношениями А и В называется множество всех кортежей t, каждый из которых принадлежит А и не принадлежит В.
Пример в языке SQL:
SELECT НОМЕР_ПОСТАВЩИКА FROM S
WHERE NOT EXISTS
(SELECT НОМЕР_ПОСТАВЩИКА FROM SP
WHERE SP.HOMEP_ПОСТАВЩИКА =
S. НОМЕР_ПОСТАВЩИКА);
— Декартово произведение
Декартовым произведением двух отношений А и В называется множество всех кортежей t,
таких, что t является конкатенацией некоторого кортежа а,
принадлежащего А, и какого-либо кортежа t, принадлежащего В.
Пример в языке SQL:
SELECT S.*, SP.*
FROM S, SP;
Специальные реляционные операции
— Селекция
Пусть theta представляет собой любой допустимый оператор сравнения скаляров, например =, ¬ =,
>, >= и т. д. Theta-ceлекцией отношения А по атрибутам Х и Y называется множество всех кортежей t
из А, таких, что истинен предикат «t. X theta t. Y». Атрибуты Х и Y должны быть определены на одном и том же домене, и для этого домена оператор theta должен иметь смысл. Вместо атрибута Y может быть специфицирована константа. Таким образом, оператор theta-селекции позволяет получать «горизонтальное» подмножество заданного отношения, т. е. подмножество таких кортежей заданного отношения, для которых удовлетворяется специфицированный предикат.
Примечание. «Theta-селекцию» часто для краткости называют просто «селекцией». Но нужно отметить, что «селекция» — это не то же самое, что оператор SELECT языка SQL.
Пример в языке SQL:
SELECT *
FROM S
WHERE ГОРОД ¬= 'Лондон';
—— Проекция
Операция проекции позволяет получать «вертикальное» подмножество заданного отношения, т. е. такое подмножество, которое получается выбором специфицированных атрибутов с последующим исключением, если это необходимо, избыточных дубликатов кортежей, состоящих из значений выбранных атрибутов.
Пример в языке SQL: .
SELECT DISTINCT ЦВЕТ, ГОРОД
FROM P;
— Соединение
Пусть theta
имеет тот же смысл, что и в случае селекции. Тогда theta-соединением отношения А по атрибуту Х с отношением В по атрибуту Y называется множество всех кортежей t, таких, что t является конкатенацией какого-либо кортежа а, принадлежащего А, и какого-либо кортежа Ь,
принадлежащего В, и предикат «а. Х theta b. Y» принимает значение «истина». При этом атрибуты А.Х и B.Y должны быть определены на одном и том же домене, и оператор theta должен иметь смысл для этого домена.
Пример в языке SQL:
SELECT S.*, P.*
FROM S, P
WHERE S. ГОРОД > Р. ГОРОД;
Если оператор theta — равенство, то соединение называется эквисоединением. Из этого определения следует, что результат эквисоединения должен включать два идентичных атрибута. Если один из этих двух атрибутов исключается, что можно осуществить с помощью проекции, результат называется естественным соединением. Под неуточненным термином «соединение» обычно понимается естественное соединение.
— Деление
В ее простейшей форме, и только она здесь рассматривается, операция деления делит отношение степени два (делимое) на отношение степени один (делитель) и продуцирует результирующее отношение степени один (частное). Пусть делимое А имеет атрибуты Х и Y, а делитель В — атрибут Y. Атрибуты A.Y и B.Y должны быть определены на одном и том же домене. Результатом деления А на В является отношение С с единственным атрибутом X, таким, что каждое значение х этого атрибута С.Х появляется как значение А.Х и пара значений (х,у)
входит в А для всех значений у, входящих в В.
Пример в языке SQL:
SELECT DISTINCT НОМЕР_ПОСТАВЩИКА FROM SP, SP1
WHERE NOT EXISTS
(SELECT НОМЕР_ДЕТАЛИ FROM P
WHERE NOT EXISTS
(SELECT * FROM SP, SP2
WHERE SP2. НОМЕР_ПОСТАВЩИКА =
SP1 .НОМЕР_ПОСТАВЩИКА
AND SP2. НОМЕР_ДЕТАЛИ = Р.НОМЕР_ДЕТАЛИ));
Здесь для простоты предполагается, что: а) отношение SP имеет только два атрибута, а именно НОМЕР_ПОСТАВЩИКА и НОМЕР_ДЕТАЛИ (атрибут КОЛИЧЕСТВО игнорируется) и б) отношение Р имеет только один атрибут — НОМЕР_ДЕТАЛИ (игнорируются атрибуты НАЗВАНИЕ, ЦВЕТ, ВЕС, ГОРОД). Первое из этих двух отношений делится на второе; в результате получается отношение с одним атрибутом НОМЕР_ПОСТАВЩИКА, в котором перечисляются номера поставщиков для тех поставщиков, которые поставляют все детали.
Целесообразно упомянуть, что из восьми рассмотренных операций только пять являются примитивами, а именно: селекция, проекция, декартово произведение, объединение и разность. Другие три операции могут быть определены через первые пять. Например, естественное соединение может быть выражено как проекция селекции декартова произведения. Однако эти три другие операции, особенно соединение, оказываются настолько полезными на практике, что хорошо было бы поддерживать их непосредственно, несмотря на то, что они не являются примитивами.
Обратимся теперь к реляционной операции присваивания. Цель этой операции заключается просто в том, чтобы дать возможность сохранять значение какого-либо алгебраического выражения, например соединения, в некотором более или менее постоянном месте. Ее можно смоделировать в языке SQL с помощью операций INSERT. . .SELECT. Предположим, например, что отношение XYZ имеет два атрибута, НОМЕР_ПОСТАВЩИКА и НОМЕР-ДЕТАЛИ. Предположим также, что в настоящее время это отношение пусто (не содержит никаких кортежей). Тогда предложение SQL:
INSERT INTO XYZ (НОМЕР_ПОСТАВЩИКА, НОМЕР_ДЕТАЛИ)
SELECT S. НОМЕР_ПОСТАВЩИКА, Р. НОМЕР_ДЕТАЛИ
FROM S, P
WHERE S. ГОРОД = Р. ГОРОД;
присваивает результат входящего в него предложения SELECT, а именно проекцию соединения, отношению XYZ.
В качестве заключения на рис. А.3 приводится сводка основных компонентов реляционной модели.
Структура данных
домены (значения)
n-арные отношения (атрибуты, кортежи)
ключи (возможные, первичные, альтернативные, внешние)
Целостность данных
1. значения первичных ключей не должны быть неопределенными
2. значения внешних ключей должны соответствовать значениям первичных ключей
(или быть неопределенными)
Манипулирование данными
реляционная алгебра
объединение, пересечение, разность, декартово произведение
селекция, проекция, соединение, деление
реляционное присваивание
Рис. А.3. Реляционная модель
