§ 1. Общие сведения
В своей деятельности инженеру приходится работать с большим количеством графических работ, весьма разнообразных по видам, содержанию, назначению, выполнению. Так, чертежи могут быть выполнены вручную и с помощью машин и автоматов, фотографированием, карандашом и тушью, на чертежной бумаге, кальке и миллиметровой бумаге, однотонные, цветные и разноцветные, простые, содержащие изображение одной детали, и сложные сборочные чертежи. Одни чертежи, содержащие изображения машин, аппаратов, автоматов, зданий и сооружений и т. д., выполняются от руки, для выполнения других нужны различные инструменты и приспособления.
Это обусловливает необходимость применения различных материалов, инструментов, приспособлений, машин и автоматов, а также методов выполнения графических работ.
§2. Материалы
Для выполнения различных видов чертежей карандашом, тушью, красками применяют чертежную бумагу марки О (обычная) и В (высшего качества). Отличительным признаком бумаги высшего качества является наличие на ней водяных знаков, видимых на просвет. Обыкновенная бумага выпускается двух видов: № 1—более высокого качества и № 2 — менее плотная и жесткая.
Для выполнения калькировочных работ с целью размножения чертежей методом светокопирования применяют прозрачную бумагу-кальку, изготовленную на бумажной или полотняной основе, а для бескалькировочного размножения чертежей — кальку карандашную. Для выполнения черновых изображений в масштабе, различных расчетно-графических работ применяют миллиметровую бумагу, а для эскизных работ — белую писчую клетчатую бумагу, обычно с размером клеток 5x5.
Чертежи, выполняемые с помощью графических автоматов и фотографированием, выполняются на листовой или рулонной чертежной бумаге, фотобумаге различных типов или специальной бумаге, изготовленной по отдельным требованиям.
Чертежные карандаши маркируются по твердости стержней от 2Т до 2М. Грифель карандаша тем тверже, чем большая цифра стоит перед буквой Т, и тем мягче, чем большая цифра стоит перед буквой М. Карандаши с грифелем средней твердости имеют обозначение ТМ. На карандашах зарубежного изготовления можно встретить вместо буквы Т буквы Н, а вместо буквы М — В.
Для определенного вида графических работ применяют соответствующую марку карандаша по твердости. Так, для выполнения чертежа в тонких линиях применяют карандаши марки Т, 21, для обводки чертежа — марки М, ТМ, для выполнения рисунков — марки М, 2М. Затачиваются карандаши на конус или «лопаточкой» на длину до 25 мм. При этом графитовый стержень должен выступать из деревянной оправы на 7—9 мм. Заточку карандашей лучше вести с помощью наждачной бумаги.
Некоторые виды чертежей на бумаге, а также чертежи на кальке (упрощенно такие чертежи называют просто кальки) для светокопирования выполняются тушью. Она выпускается, как правило, в флаконах и различается по качеству и цвету.
Большинство чертежей выполняется черной тушью. В период работы тушь в флаконах необходимо предохранять от высыхания. Загустевшую тушь разбавляют кипяченой водой или нашатырным спиртом. Качество линий, проведенных тушью, зависит от степени ее разбавления, поэтому, разбавляя тушь, необходимо контролировать качество проводимых линий.
Чертежные резинки применяются двух типов: для стирания линий, выполненных карандашом, и для стирания линий, выполненных тушью. Резинка, применяемая для работы с карандашом, мягкая и при стирании снимает с бумаги только частички графита, не нанося ей значительных повреждений; резинка, применяемая для стирания туши, содержит твердые добавки и при стирании шлифует верхний слой бумаги.
Для получения цветных изображений на чертежах применяют акварельные краски, состоящие из тонкого красящего вещества и связующих. Они разводятся на воде. Особенностью этих красок является то, что при нанесении их слоями один на другой и при смешивании можно получить необходимые оттенки. Иногда применяют краски клеевые и гуашь, которые разводятся на воде. Но они не прозрачные и при наложении одного слоя краски на другой верхний слой полностью скрывает нижний.
§ 3. Инструменты
Графические работы выполняются с помощью чертежных инструментов. Набор таких инструментов, размещенный в специальном футляре, называется готовальней. Выпускаются различные типы готовален. Для выполнения чертежно-конструкторских и копировальных работ карандашом и тушью выпускаются универсальные готовальни (У), имеющие в своем наборе различное количество инструментов: У9, У9-Л, У10, У11, У14, У14-Л, У15, У24, У32. Цифра указывает на количество инструментов в наборе.
Для выполнения чертежно-конструкторских работ карандашом выпускаются готовальни: конструкторская (К), конструкторская большая (КБ), конструкторская малая (КМ и КМ-Л). Для выполнения ученических работ выпускают школьные готовальни (Ш). Лучшими считаются наборы чертежных инструментов, изготовленных из латуни (кроме У9, У14, КМ и Ш).
Основными чертежными инструментами в составе готовален являются следующие.
Циркуль чертежный предназначен для проведения окружностей и дуг различных радиусов (не менее 3—4 мм). К циркулю прилагается вставка игольная, рейсфедер циркульный, карандашная ножка и удлинитель, позволяющий осуществлять проведение окружностей диаметром до 450 мм. При работе циркулем иголку и рейсфедер (или карандашную вставку) следует устанавливать перпендикулярно к поверхности бумаги.
Циркуль разметочный предназначен для измерения расстояния и откладывания длин на чертеже. При работе с циркулем иголки обеих ножек должны быть одинаковой высоты.
Кронциркуль падающий служит для вычерчивания окружностей малого диаметра. В нем для удобства работы вращающаяся ножка выполнена свободно перемещающейся вдоль оси кронциркуля. К кронциркулю прилагаются вставка карандашная и рейсфедер циркульный.
Кривоножка служит для проведения кривых линий от руки или под лекало. Состоит из полой пластмассовой ручки, оси с винтом фиксации ножки в неподвижном положении и рейсфедера с кривоножкой.
Рейсфедер с широкими щечками и делительной гайкой применяется для проведения линий толщиной до 1,5 мм. Регулирование толщины линий осуществляется с помощью винта и гайки с делениями. I
Центрик применяется при проведении концентрических окружностей. Он устроен в виде кнопки, в головке которой выполнено углубление для иглы ножки циркуля.
§ 4. Принадлежности и приборы
При выполнении графических работ применяют различные принадлежности и приборы, облегчающие труд чертежника, создающие удобства и повышающие производительность труда. На рис. 1 показана чертежная доска с расположенными на ней чертежными принадлежностями.
Чертежная доска служит для прикалывания к ней кнопками бумаги. Она представляет собой деревянный щит, состоящий из продольных дощечек, стянутых торцевыми наружными планками и скрепленных клеем. Рабочую поверхность представляют продольные дощечки, изготовляемые из дерева мягких пород — ольхи или липы. Доски изготовляют различных размеров. Например, чертежная доска №2 имеет длину 1000 мм, ширину 650 мм и толщину 20 мм.
Рейсшина состоит из длинной линейки и двух коротких планок-перекладин. Одна из перекладин соединена с длинной линейкой неподвижно, вторая может быть повернута по отношению к большой линейке на любой угол. Таким образом с помощью рейсшины можно проводить параллельные горизонтальные и наклонные линии.

Рис. 1
Мерительная линейка служит для измерения длин на чертеже. Она изготовляется из твердого дерева и в поперечном сечении имеет форму симметричной трапеции. Линейка снабжена белыми целлулоидными полосками, наклеенными на наклонных ее гранях и имеющими прямолинейную равномерную шкалу с ценой деления 1 мм.
Угольники служат для работы с ними отдельно или в сочетании с рейсшиной. С их помощью можно выполнить различные геометрические построения; проведение ряда параллельных линий, построение взаимно перпендикулярных линий, вычерчивание углов и многоугольников, деление окружности на заданное количество равных участков.
Лекала служат для вычерчивания кривых линий. Они представляют собой тонкие пластинки криволинейного очертания, дающие возможность провести кривые линии, которые не могут быть выполнены с помощью циркуля. Лекала изготовляют с различной кривизной линий. Для вычерчивания лекальной кривой лекало подбирают так, чтобы его кромка совпадала не менее чем с четырьмя точками кривой; при этом соединяют линией только две из них и далее лекало передвигают к последующим точкам.
Транспортир применяют для измерения и откладывания углов на чертеже.
Трафареты и шаблоны применяют для сокращения затрат труда и времени на выполнение отдельных видов графических работ. По форме они могут быть весьма разнообразными в зависимости от их предназначения. С помощью трафаретов и шаблонов могут быть выполнены надписи, вычерчены окружности, прямоугольники, углы, знаки.
Чертежные приборы служат для облегчения труда чертежника, снижения затрат времени на выполнение графических работ. В настоящее время применяются различные конструкции чертежных приборов. Они позволяют заменить одновременно рейсшину, транспортир, угольник, линейку.
Чертежный прибор (рис. 2) включает две линейки, установленные под углом 90° друг к другу.
С помощью специальной поворотной головки линейки можно расположить под различными углами наклона к заданным линиям. Головка связана системой подвижных рычагов, позволяющей перемещать ее по полю чертежа, с кронштейном-струбциной, с помощью которой и крепится к чертежной доске. Применение такого прибора сокращает затраты времени примерно на одну четверть против выполнения чертежей с применением рейсшины.
Для механизации графических работ применяются также более сложные чертежные станки и комбайны.

Рис. 2
Прибор для штриховки служит для проведения ряда параллельных линий, служащих штриховкой отдельных участков чертежа. Он представляет собой две линейки, одна из которых своим концом шарнирно прикреплена к другой с возможностью перемещения шарнира вдоль второй линейки на заданную величину.
§ 5. Графические автоматы
В последние годы для решения различных задач инженерной графики применяют ЭВМ различных типов в зависимости от характера решаемой задачи. Для этой цели составляют план решения задачи, алгоритм и пишут на заданном алгоритмическом языке программу. Подготовленные данные вводят в ЭВМ и получают ответ, например в виде координат искомых точек. Такое применение ЭВМ позволяет значительно ускорить решение графических задач, но не решает задачу облегчения чертежно-конструкторского труда.
Для механизации и автоматизации конструкторско-графических работ все более широкое применение находят графические автоматы различных типов. Одни из них позволяют получать и размножать чертежи непосредственно на бумаге (графопостроители), другие — получить их изображение на экране (графические дисплеи). Автоматизированные графические устройства могут работать в индивидуальном режиме с соответствующей подготовкой для этого исходных данных и в режиме связи с ЭВМ, когда проектировщик может выбрать оптимальные варианты решения задач. Графические автоматы находят широкое применение в системах автоматизированного проектирования.
§ 6. Методы выполнения графических работ
При выполнении значительного объема графических работ необходимо прежде всего правильно организовать рабочее место чертежника. Чертежная доска, на которой закрепляется бумага, должна быть расположена примерно на 15° в сторону чертежника. При большем наклоне чертежные инструменты могут соскальзывать с чертежной доски.
Перед началом работы следует собрать инструменты, которые будут необходимы для выполнения конкретного чертежа. Их необходимо протереть сухой тряпочкой из хлопчатобумажной ткани. Отобранные инструменты должны располагаться так, чтобы они не мешали работе и в то же время чтобы можно было быстро выбрать среди них необходимый.
До начала выполнения чертежа необходимо заточить несколько карандашей. Это позволит избежать потерь времени на их заточку в процессе работы и работать, не отрываясь от чертежа. Нужно проверить также, чтобы на столе не было ничего лишнего и свет падал с левой стороны.
Прикалывая чертежную бумагу к доске, первую кнопку следует расположить в верхнем левом углу и выровнять верхний срез листа по кромке рейсшины. Второй кнопкой закрепляют правый нижний угол листа, потом закрепляют оставшиеся углы.
Чертежи могут быть выполнены карандашом или тушью. И в том и в другом случае производят подготовку чертежа карандашом и потом обводят его карандашом или тушью.
В производственных условиях чертежи в большинстве случаев выполняют карандашом. Тушью выполняют чертежи в специальных случаях, например для размножения путем светокопирования или фотографирования. К особенностям выполнения чертежей тушью относится то, что на глянцевой бумаге обводить линии тушью более трудно, чем на обычной чертежной бумаге, имеющей шероховатую поверхность. С другой стороны, линии, проведенные тушью, значительно легче подчистить в случае необходимости исправлений.
Обводка чертежа карандашом отличается тем, что чертеж в этом случае трудно сохранить чистым, а вычистить резинкой можно только части поля листа, не занятые изображениями. Это требует в процессе подготовки чертежа тщательного соблюдения чистоты на чертеже и избежания проведения дополнительных, лишних, случайных линий.
Недостатком обводки чертежей карандашом является то, что трудно провести линии одинаковой толщины, а также одинаковой черноты с помощью циркуля.
Подготовка чертежа заключается в построении всех его фигур и выполнении надписей тонкими линиями. Для этих работ подбирают твердые карандаши марки 2Т или ЗТ с остро отточенным грифелем.
Далее отбирают характерные точки изображения, соединив которые, можно получить изображаемую фигуру. При нанесении точек с помощью циркуля-измерителя их можно легко накалывать, а при нанесении с помощью линейки отмечать легким уколом карандаша или маленьким кружком. При построении точек циркулем они наносятся в виде засечек. Полученные точки соединяют прямыми или кривыми линиями и получают контур изображения, на который наносят остальные необходимые линии.
После выполнения построения чертеж следует тщательно проверить, выявить и удалить случайные, лишние или неправильные линии. Причем если обводка чертежа будет выполняться карандашом, то удалить эти линии следует до обводки, если же тушью — то после. Перед обводкой тушью их необходимо зачеркнуть карандашом. До обводки чертежа следует только в необходимых случаях пользоваться резинкой, так как это приводит к загрязнению чертежа и повреждению поверхности бумаги, на которую при обводке плохо наносится тушь.
Для ускорения работы по обводке чертежа сначала подряд проводят горизонтальные линии на всех изображениях, потом вертикальные, за ними наклонные одного направления, потом второго и т. д. Сначала проводят сплошные основные толстые линии, за ними, например, штриховые, сплошные тонкие и т. д. В последнюю очередь заполняют графы основной надписи, наносят технические требования и размерные числа.
После окончания обводки чертежа его необходимо снова тщательно проверить для выявления возможных ошибок и упущений. Проверку следует вести по отдельным вопросам в пределах всего чертежа, например, полностью ли обведены нужные линии, везде ли нанесены стрелки на размерных линиях, на всех ли размерных линиях поставлены размеры, не проведены ли лишние линии и др.
Следует отметить, что выполнение графических работ в основной массе осуществляется карандашом, поэтому уместно напомнить несколько общих правил работы с ним. Затачивать карандаш следует с конца свободного от надписи, чтобы сохранить его маркировку.
Подбор твердости грифеля карандаша и правильность его заточки при наличии заданного сорта бумаги должны обеспечивать получение линии четких, хорошо видимых, необходимой толщиной. Нанесение линий плохо видимых, бледных, серых приводит к утомлению зрения чертежника.
Необходимо постоянно следить за сохранением конусности и длины грифеля, постоянно подтачивать его. Укорочение конуса приводит к утолщению линий.
Подбор карандаша при соответствующем сорте бумаги обеспечивает проведение линий, исключающее вдавливание карандаша в бумагу. Это дает возможность при необходимости стереть линию без оставления следов.
При проведении линий карандашом по линейке, рейсшине или угольнику карандаш должен быть расположен в плоскости, перпендикулярной плоскости чертежа или слегка наклонной от себя.
В процессе выполнения чертежа горизонтальные линии рекомендуется проводить по верхней кромке линейки или рейсшины слева направо, а вертикальные — снизу вверх.
При выполнении надписей и размерных цифр на поле чертежа под руку с карандашом необходимо подкладывать чистый лист бумаги, что исключает загрязнение чертежа.
Можно дать некоторые рекомендации и по обводке чертежа тушью, которая осуществляется на чертежной бумаге или на кальке. Обводка на кальке несколько труднее из-за ее глянцевой поверхности. Четкость линии обеспечивается правильной работой с рейсфедером и подбором концентрации туши путем ее разбавки. Выбрав лист бумаги, следует провести на нем несколько пробных линий. Если тушь засыхает в рейсфедере, ее необходимо разбавить, но не доводить до состояния, когда линии будут расплываться.
В заключение можно напомнить также общий ход выполнения чертежа. Начинают выполнять чертеж с вычерчивания рамки формата, выделения поля чертежа и места расположения основной надписи.После этого на поле чертежа намечают расположение изображений — наносят контуры изображения или габаритные очерки. Это дает возможность оценить правильность выбора места расположения изображений и при необходимости внести изменения. Если изображения симметричны, проводят оси симметрии; отмечают центры окружностей штрихпунктирными линиями; наносят остальные элементы изображения. При этом сначала вычерчивают дуги окружностей, а потом линии, касательные к ним.
§ 7. Общие сведения
Все правила выполнения чертежей, действующие в настоящее время, отражены в государственных стандартах (ГОСТ) Единой системы конструкторской документации (ЕСКД), учитывающей многие рекомендации международных организаций по стандартизации.
Все стандарты, предусмотренные ЕСКД, распределяются по следующим классификационным группам:
0 — общие положения;
1 — основные положения;
2 — классификация и обозначения изделий в конструкторских документах;
3 — общие правила выполнения чертежей;
4 — правила выполнения чертежей в машиностроении и приборостроении;
5 — правила обращения конструкторских документов (учет, хранение, дублирование, внесение изменений);
6 — правила выполнения эксплуатационной и ремонтной документации;
7 — правила выполнения схем;
8 — правила выполнения строительных документов и документов судостроения;
9 — прочие стандарты.
В ЕСКД все стандарты имеют определенную структуру обозначений и названий. Например, ГОСТ 2.303—68 «Линии» означает, что стандарт входит в комплекс ЕСКД, которому присвоен номер 2, номер стандарта — 303 (3 — шифр классификационной группы, 03 — порядковый номер стандарта в группе), год регистрации — 1968, название — «Линии».
В курсе инженерной графики нашли отражения требования стандартов, входящих в группы 1, 2, 3, 4, 7.
Вполне понятно, что все стандарты ЕСКД разработаны для промышленности и не учитывают особенностей выполнения чертежей в учебных заведениях, поэтому при выполнении учебных чертежей допускаются некоторые отклонения от стандартов. При выполнении чертежей необходимо руководствоваться требованиями, установленными «Единой системой конструкторской документации», к форматам, основным надписям, масштабам, линиям, шрифтам и др.
§ 8. Форматы
Все чертежи должны выполняться на листах бумаги стандартного формата. Форматы листов бумаги определяются размерами внешней рамки чертежа (рис. 3). Она проводится сплошной тонкой линией. Линия рамки чертежа проводится сплошной толстой основной линией на расстоянии 5 мм от внешней рамки. Слева для подшивки оставляют поле шириной 20 мм. Обозначение и размеры сторон форматов установлены ГОСТ 2.304—68. Данные об основных форматах приведены в табл. 1.
Таблица 1
|
Обозначение формата | |||||||||||
|
АО |
А1 |
А2 |
A3 |
А4 | |||||||
|
Размеры сторон листа, мм | |||||||||||
|
1189x841 |
594 х 841 |
594 х 420 |
297 х 420 |
297 х 210 | |||||||
Основные форматы получают из формата АО путем последовательного деления на две равные части параллельно меньшей стороне. При необходимости допускается применять формат А5 с размерами сторон 148 х 210мм. Допускается также применение дополнительных

Рис. 3
форматов. Они образуются увеличением сторон основных форматов на величину, кратную размерам сторон формата А4 (рис. 4).
Допускаются следующие отклоления сторон формата при размерах сторон: до 150 ±1,5, от 150 до 600 ±2,0, свыше 600 ±3,0.
§ 9. Основная надпись
Основная надпись чертежа располагается в правом нижнем углу формата (см. рис. 3). Форма, размеры и содержание граф основной надписи установлены ГОСТ 2.104—68. В основной надписи указывают: в графе 1 — наименование изделия; в графе 2 — обозначение чертежа; в графе 3 — материал детали; в графе 4 — наименование предприятия-изготовителя чертежа.
В левом верхнем углу чертежа, в рамке размером 14 х 70 записывается обозначение чертежа, данное в графе 2 рамки основной надписи, повернутое на 180°.
На форматах, больших А4, основная надпись может быть расположена как по короткой, так и по длинной стороне. При расположении основной надписи вдоль короткой стороны повернутое обозначение чертежа располагается в правом верхнем углу по длинной стороне.

Рис. 4
На формате А4 основная надпись располагается только вдоль его короткой стороны.
§ 10. Масштабы
Изображение предмета на чертеже может быть выполнено в натуральную величину, уменьшенным или увеличенным. Отношение всех линейных размеров изображения предмета на чертеже к их натуральной величине называется масштабом.
ГОСТ 2.302—68 устанавливает следующий ряд масштабов изображений на чертежах:
масштабы уменьшения —1:2; 1 :2,5; 1:4; 1:5; 1 : 10; 1:15; 1 :20; 1 :25; 1 : 40; 1 : 75; 1 : 100; 1 : 200;
натуральная величина — 1:1;
масштабы увеличения — 2 : 1; 2,5 : 1; 4:1; 5:1; 10 : 1; 40 : 1; 50: 1; 100: 1;
Изображение предмета на чертеже в масштабе увеличения или уменьшения не предусматривает целей определения его размеров, оно вызвано только необходимостью правильного зрительного восприятия формы изображаемого предмета, поэтому, независимо от масштаба изображения, размеры на чертеже проставляются действительные.
Масштаб в основной надписи чертежа обозначается по типу 1:1; 1 : 2; 2 : 1 и т. д. Масштабы изображения, отличающиеся от указанного в основной надписи чертежа, указывают непосредственно после надписи, относящейся к данному изображению, по типу: А (1 : 10), А —А (2:5).
§ 11. Линии
Основными элементами любого чертежа являются линии. В зависимости от их назначения они имеют соответствующие тип и толщину. Изображения предметов на чертеже представляют собой сочетание различных типов линий.
Типы линий, их назначение и толщина установлены ГОСТ 2.303—68 (табл. 2). Сплошная толстая основная линия принята за исходную. Толщина ее S должна выбираться в пределах от 0,6 до 1,5 мм. Она выбирается в зависимости от величины и сложности изображения, формата и назначения чертежа. Исходя из толщины сплошной толстой основной линии выбирают толщину остальных линий при условии, что для каждого типа линий в пределах одного чертежа на всех изображениях она будет одинаковой.
Таблица 2
|
Наименование |
Толщина линии по отношению к толщине основной линии |
Основное назначение | |||||
|
1 . Сплошная толстая линия основная |
0,6... 1,5 мм S |
Линии видимого контура; линии перехода видимые; линии контура сечения (вынесенного и входящего в состав разреза) | |||||
|
2. Сплошная тонкая |
От S/2 до S/2 |
Линии контура наложенного сечения; линии размерные и выносные; линии штриховки; линии-выноски; полки линий-выносок и подчеркивания надписей; линии для изображения пограничных деталей («обстановка»); линии ограничения выносных элементов на видах, разрезах и сечениях; линии перехода воображаемые (следы плоскостей, линии построения характерных точек при специальных построениях) | |||||
|
3. Сплошная волнистая |
От S/3 до S/2 |
Линии обрыва; линии разграничения вида и разреза | |||||
|
4. Штриховая |
От S/3 до S/2 |
Линии невидимого контура; линии перехода невидимые | |||||
|
5. Штрих- пунктирная тонкая |
От S/3 до S/2 |
Линии осевые и центровые; линии сечений, являющиеся осями симметрии для наложенных или вынесенных сечений | |||||
|
6. Штрихпунк-тирная утолщенная |
От S/3 до (2/3) S |
Линии, обозначающие поверхности, подлежащие термообработке или покрытию; линии для изображения элементов, расположенных перед секущей плоскостью («наложенная проекция») | |||||
|
7. Разомкнутая 8. Сплошная тонкая с изло- |
От S до 1,5 S От S/3 до S/2 |
Линии сечений Длинные линии обрыва | |||||
|
мами 9. Штрихпунк-тирная с двумя точками тонкая |
От S/3 до S/2 |
Линии сгиба на развертках; линии для изображения частей изделий в крайних или промежуточных положениях; линии для изображения развертки, совмещенной с видом | |||||
Примечание.
Толщина линий S/ 3 допускается только для чертежей, выполненных тушью, на форматах с А4 по А2.
В штриховых линиях штрихи должны быть равной длины, а промежутки между ними одинаковыми. Штрихпунктирные линии должны пересекаться и заканчиваться штрихами. Центровые линии должны выходить за очертания окружности на 3...5 мм. Для окружностей, диаметр которых 12 мм и менее, центровые линии вычерчивают сплошными тонкими.
Примеры применения различных типов линий на чертеже приведены на рис. 5.
Линии могут иметь специальное назначение, например, для изображения резьбы, шлицев границ, зон с различной шороховатостью поверхности и др. Их применение регламентируется специальными стандартами ЕСКД.
Качество чертежа в значительной степени зависит от правильного выбора типа линий, соблюдения одинаковой толщины обводки, длины штрихов и расстояния между ними, аккуратности их проведения.
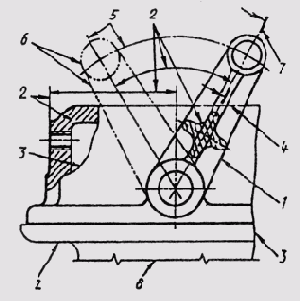
Рис. 5
§ 12. Надписи на чертежах
Все надписи на чертежах должны выполняться стандартным чертежным шрифтом. Чертежный шрифт применяют также для выполнения надписей на других технических документах. При этом буквы шрифта, цифры, отдельные надписи и текст выполняют от руки. Отдельные надписи могут состоять из одних прописных букв. Цифры, встречающиеся в тексте, также выполняются высотой, равной высоте прописных букв.
Все надписи и размерные числа на чертежах должны быть четкими и ясными. Выполняются надписи шрифтами, предусмотренными ГОСТ 2.304—81 «Шрифты чертежные». Эти шрифты включают русский, латинский и греческий алфавиты, а также арабские и римские цифры.
Стандарт устанавливает следующие размеры шрифта: (1,8); 2,5; 3.5;5;7; 10; 14;20;28;40. Размер шрифта h определяет высоту прописных (заглавных) букв и цифр в миллиметрах.
Данные, касающиеся шрифтов типов A (d = h/14) и Б (d = h/10), приведены соответственно в табл. 3 и 4.
Таблица 3
|
Параметры шрифта |
Обоз- начение |
Относи- тельный размер, d |
Размеры, мм | ||||||||||||||||||
|
Размер шрифта — высота прописных букв |
h |
14d |
2,5 |
3,5 |
5,0 |
7,0 |
10,0 |
14,0 |
20,0 | ||||||||||||
|
Высота строчных букв |
с |
10d |
1,8 |
2,5 |
3,5 |
5,0 |
7,0 |
10,0 |
14,0 | ||||||||||||
|
Расстояние между буквами |
а |
2d |
0,35 |
0,5 |
0,7 |
1,0 |
1,4 |
2,0 |
2,8 | ||||||||||||
|
Максимальный шаг строк (высота вспомогательной сетки) |
d |
22d |
4,0 |
5,5 |
8,0 |
11,0 |
16,0 |
22,0 |
31,0 | ||||||||||||
|
Минимальное расстояние между словами |
е |
6d |
1,1 |
1,5 |
2,1 |
3,0 |
4,2 |
6,0 |
8,4 | ||||||||||||
|
Толщина линий шрифта |
d |
d |
0,18 |
0,25 |
0,35 |
0,5 |
0,7 |
1,0 |
1,4 | ||||||||||||
Стандартом установлены следующие два типа шрифта в зависимости от толщины d линий шрифта: тип A (d = 1 /14h) без наклона и с наклоном около 75° к горизонтальной строке; тип Б (d= 1/10h) без наклона и с наклоном под 75°. На рис. 6 приведена форма букв русского алфавита и арабских цифр, выполненных шрифтом Б без наклона.

Рис 6.
Таблица 4
Параметры шрифта |
Обозна- чение |
Относи- тельный размер, d |
Размеры, мм |
|||||||||
Размер шрифта — высота прописных букв |
h |
10d |
1,8 |
2,5 |
3,5 |
5,0 |
7,0 |
10,0 |
14,0 |
20,0 |
||
Высота строчных букв |
с |
7d |
1,3 |
1,8 |
2,5 |
3,5 |
5,0 |
7,0 |
10,0 |
14,0 |
||
Расстояние между буквами |
а |
2d |
0,35 |
0,5 |
0,7 |
1,0 |
1,4 |
2,0 |
2,8 |
4,0 |
||
Минимальный шаг строк (высота вспомогательной сетки) |
b |
17d |
3,1 |
4,3 |
6,0 |
8,5 |
12,0 |
17,0 |
24,0 |
34,0 |
||
Минимальное расстояние между словами |
е |
6d |
1,1 |
1,5 |
2,1 |
3,0 |
4,2 |
6,0 |
8,4 |
12,0 |
||
Толщина линий шрифта |
d |
d |
0,18 |
0,25 |
0,35 |
0,5 |
0,7 |
1,0 |
1,4 |
2,0 |
||
При выполнении надписей на чертежах стандартными шрифтами расстояние а между буквами, соединение линий, которые не параллельны между собой (например, Г и А, А и Т и т. д.), уменьшается на половину, т. е. на толщину плиний шрифта. Для всего текста толщина линий одного шрифта должна быть одинакова.
Выполняемые чертежи часто имеют большое количество буквенных и цифровых надписей. Их необходимо, как правило, располагать горизонтально. Следует избегать расположения надписей внутри контура проекций (кроме размерных чисел). Если надпись наносится под линией или подчеркивается линией, то она должна отстоять от нее примерно на 1 мм.
Если надпись пересекает линию, то в месте пересечения линию необходимо прервать. При заполнении граф основной надписи и других графических документов надпись необходимо располагать по возможности на одинаковом расстоянии от ограничивающих графу линий.
§ 13. Основные правила нанесения размеров на чертеже
По изображениям предмета на чертеже судят о его величине и величине его отдельных частей. Основанием для этого служат размерные числа, независимо от того, в каком масштабе и с какой точностью

Рис. 7

Рис. 8

Рис. 9

Рис. 10

Рис. 11

Рис. 12

Рис. 13
выполнены изображения. Правила нанесения размеров на чертежах установлены ГОСТ 2.307—68.
Размеры на чертеже указывают размерными числами, размерными и выносными линиями. Размерные числа на чертежах, как правило, указывают в миллиметрах без указания единиц измерения. В тех случаях, когда необходимо применять другие единицы измерения длины, их показывают после размерного числа.
Размерные числа наносят над размерной линией, возможно ближе к ее середине. Зазор между размерным числом и размерной линией должен быть около 1,0 мм. Высоту цифр размерных чисел принимают не менее 3,5 мм (рис. 7).
Размерная линия проводится параллельно отрезку, размер которого над ней наносится. Ее проводят между выносными линиями, проведенными перпендикулярно размерным. Допускается размерные линии проводить непосредственно к линиям видимого контура, осевым и центровым. В отдельных случаях размерная линия может проводиться не перпендикулярно выносной (рис. 8). Размерные линии ограничивают стрелки (рис. 9). В отдельных случаях их проводят не полностью, а с обрывом стрелки с одной стороны (рис. 10). Размер стрелки выбирают от принятой на чертеже толщины сплошной толстой основной линии. В пределах одного чертежа величина стрелок должна быть по возможности одинаковой. Не рекомендуется в качестве размерных линий использовать контурные, осевые, центровые и выносные линии.
Если длина размерной линии мала для размещения стрелок, то размерную линию продолжают за выносные линии, и размеры наносят, как показано на рис. 11.
Выносные линии проводят от границ измерений, они являются вспомогательными и служат для размещения между ними размерных линий. Выносные линии следует по возможности располагать вне контура изображения, перпендикулярно прямолинейному отрезку, размер которого необходимо указать.
Выносные линии должны выходить за концы стрелок размерных линий на 1...5 мм (рис. 12).
Минимальное расстояние от размерной линии до параллельной ей линии должно быть 10 мм, а между параллельными размерными линиями — 7 мм.
Угловые размеры на чертежах проставляются в градусах, минутах и секундах с указанием единиц измерения. Размер угла наносят над размерной линией, которая проводится в виде дуги с центром в его вершине. Выносные линии в этом случае проводятся радиально (рис. 13).
При различных наклонах размерных линий размерные числа линейных размеров располагают так, как показано на рис. 14, а, а угловые размеры — как показано на рис. 14, б. Если размерная линия будет находиться в зоне, которая на чертеже заштрихована, размерные числа наносят на полках линий-выносок (рис. 15).
Если для написания размерного числа мало места над размерной линией или это место занято другими элементами изображения и впи-

Рис. 14

Рис. 15

Рис. 16

Рис. 17
сать в него размерное число невозможно, размерное число наносят по одному из вариантов, приведенных на рис. 16.
С целью упрощения ряда изображений, создания удобств для чтения чертежа стандарт предусматривает применение условных обозначений в виде букв латинского алфавита и графических знаков, которые ставятся перед размерными числами. На чертежах применяются

Рис. 18

Рис. 19

Рис. 20

Рис. 21

Рис. 22

Рис. 23

Рис. 24
знаки и буквы для обозначения диаметра и радиуса, длины дуги и квадрата, уклона и конусности, сферы, толщины и длины детали.
Перед размерным числом диаметра наносится знак 0 (рис. 17). Причем между знаком и числом никаких пропусков не предусмотрено. Для окружностей малого диаметра размерные линии стрелки и сам размер наносят по одному из вариантов, приведенных на рис. 18.
Перед размерным числом радиуса дуги всегда ставится знак в виде прописной латинской буквы R. Размерную линию в этом случае проводят по направлению к центру дуги и ограничивают только одной стрелкой, упирающейся в дугу или ее продолжение (рис. 19).
Если величина радиуса на чертеже менее 6 мм, стрелку рекомендуется распо-

Рис. 25
лагать с внешней стороны дуги. При необходимости задания положения центра дуги его отмечают пересечением центровых или выносных линий (рис. 20). В тех случаях, когда на чертеже изображена дуга большого радиуса, для которой центр можно не обозначать, размерную линию обрывают, не доводя до центра (рис. 21). Если же в этом случае центр необходимо отметить, допускается приближать его к дуге (рис. 22). Размерная линия в этом случае показывается с изломом 90°, и оба участка размерной линии проводятся параллельно. Не следует располагать на одной прямой размерные линии, выходящие из одного центра и предназначенные для обозначения размерных дуг. Радиусами рекомендуется обозначать дуги до 180°; дуги, величина которых составляет более 180°, обозначаются диаметром.
Знак дуги наносится над размерным числом (рис. 23). Длину дуги задают в линейных единицах, а размерное число, обозначающее дугу, наносится над размерной линией в соответствии с обычными требованиями.
Для простановки размеров квадрата применяют соответствующий знак D, высота которого равна 7/10 высоты размерного числа (рис. 24, а). При ином расположении квадрата наносят размеры его сторон (рис. 24, б). Следует отметить, что знак квадрата наносят только на том изображении, на котором он проецируется в линию.
Знак конусности поверхности наносится на полке линии-выноски, расположенной параллельно оси конуса или на оси конуса (рис. 25, а). Знак конусности располагают так, чтобы его острый угол был направлен в сторону вершины конуса. Величину конусности определяют отношением разности диаметров двух поперечных сечений конуса к расстоянию между этими сечениями, т. е. k = D — dll, где D — диаметр большого сечения; d — диаметр меньшего сечения; l — расстояние между сечениями. Конусность указывают в виде простого дробного числа (рис. 25, б).
Знак уклона прямой указывают на полке линии-выноски. Уклон i представляет собой тангенс угла между данной прямой и горизонтальной или вертикальной прямой (рис. 26, а).
Знак уклона располагается

Рис. 26

Рис. 27

Рис. 28
так, чтобы острый угол его был направлен в сторону уклона прямой (рис. 26, б). Уклон, как и конусность, на чертеже задают простой дробью, в процентах или в промилях.
Для обозначения сферы на чертеже применяют знак диаметра или радиуса. В тех случаях, когда по чертежу сферу трудно отличить от других поверхностей, перед знаком радиуса или диаметра допускается добавлять слово «Сфера». Надпись на чертеже выполняется по типу «Сфера диаметр 17» или «Сфера R10» (рис. 27).
Простые плоские детали изображаются в виде одной проекции. В этих случаях ее толщину обозначают строчной буквой s и надпись на чертеже выполняется по типу s2 и располагается на полке линии-выноски (рис. 28, а). Длину предмета указывают буквой / (рис. 28, б).
Фаски на чертежах наносят двумя линейными размерами (рис. 29, а) или одним линейным и одним угловым (рис. 29, б). В том случае, если

Рис. 29
угол наклона образующей конуса равен 45°, применяют упрощенное обозначение фаски, когда размерная линия проводится параллельно оси конуса, а надпись выполняется по типу «2 х 45» (рис. 29, в).
§ 14. Общие сведения
При выполнении графических работ приходится решать многие задачи на построение. Наиболее встречающиеся при этом задачи — деление отрезков прямой, углов и окружностей на равные части, построение различных сопряжений прямых с дугами окружностей и дуг окружностей между собой. Сопряжением называют плавный переход дуги окружности в прямую или в дугу другой окружности.
Наиболее часто встречаются задачи на построение следующих сопряжений: двух прямых дугой окружности (скруглением углов); двух дуг окружностей прямой линией; двух дуг окружностей третьей дугой; дуги и прямой второй дугой.
Построение сопряжений связано с графическим определением центров и точек сопряжения. При построении сопряжения широко используются геометрические места точек (прямые, касательные к окружности; окружности, касательные друг к другу). Это объясняется тем, что они основаны на положениях и теоремах геометрии.
§ 15. Деление отрезка прямой
Чтобы разделить заданный отрезок АВ на две равные части, точки его начала и конца принимают за центры, из которых проводят дуги радиусом, по величине превышающим половину отрезка АВ. Дуги проводят до взаимного пересечения, где получают точки С и D. Линия, соединяющая эти точки, разделит отрезок в точке К на две равные части (рис. 30, а).
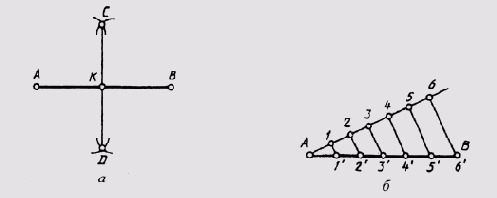
Рис. 30
Чтобы разделить отрезок АВ на заданное количество равных участков п, под любым острым углом к АВ проводят вспомогательную прямую, на которой из общей заданной прямой точки откладывают п равных участков произвольной длины (рис. 30, б). Из последней точки (на чертеже — шестой) проводят прямую до точки В и через точки 5, 4, 3, 2, 1 проводят прямые, параллельные отрезку 6В. Эти прямые и отсекут на отрезке АВ заданное число равных отрезков (в данном случае 6).
§ 16. Деление окружности
Чтобы разделить окружность на четыре равные части, проводят два взаимно перпендикулярных диаметра: на пересечении их с окружностью получаем точки, разделяющие окружность на четыре равные части (рис. 31, а).
Чтобы разделить окружность на восемь равных частей, дуги, равные четвертой части окружности, делят пополам. Для этого из двух точек, ограничивающих четверть дуги, как из центров радиусов окружности выполняют засечки за ее пределами. Полученные точки соединяют с центром окружностей и на пересечении их с линией окружности получают точки, делящие четвертные участки пополам, т. е. получают восемь равных участков окружности (рис. 31, б).
На двенадцать равных частей окружность делят следующим образом. Делят окружность на четыре части взаимно перпендикулярными диаметрами. Приняв точки пересечения диаметров с окружностью А, В, С, D за центры, величиной радиуса проводят четыре дуги до пересечения с окружностью. Полученные точки 1, 2, 3, 4, 5, 6, 7, 8 и точки А, В, С, D разделяют окружность на двенадцать равных частей (рис. 31, в).
Пользуясь радиусом, нетрудно разделить окружность и на 3, 5, 6, 7 равных участков.
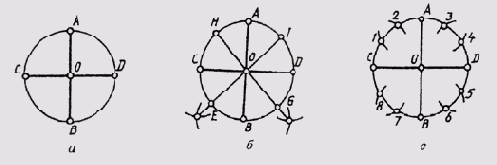
Рис. 31
§ 17. Скругление углов
Сопряжение двух пересекающихся прямых дугой заданного радиуса называют скруглением углов. Его выполняют следующим образом (рис. 32). Параллельно сторонам угла, образованного данными
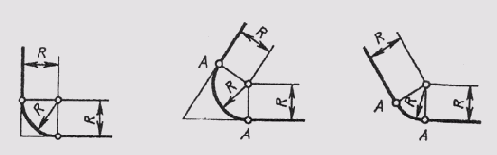
Рис. 32
прямыми, проводят вспомогательные прямые на расстоянии, равном радиусу. Точка пересечения вспомогательных прямых является центром дуги сопряжения.
Из полученного центра О опускают перпендикуляры к сторонам данного угла и на пересечении их получают точки сопряжения А а В. Между этими точками проводят сопрягающую дугу радиусом R из центра О.
§ 18. Сопряжение дуг окружностей прямой линией
При построении сопряжения дуг окружностей прямой линией можно рассмотреть две задачи: сопрягаемая прямая имеет внешнее или внутреннее касание. В первой задаче (рис. 33, а) из центра дуги
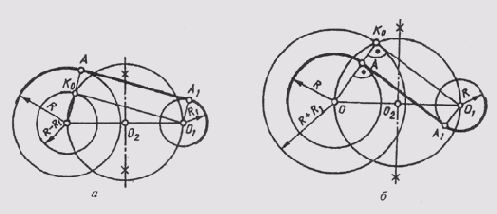
Рис. 33
меньшего радиуса R1 проводят касательную вспомогательной окружности, проведенной радиусом R — RI. Ее точку касания Ко используют для построения точки сопряжения А на дуге радиуса R.
Для получения второй точки сопряжения А1 на дуге радиуса R1 проводят вспомогательную линию О1 А1 параллельно О А. Точками A и А1будет ограничен участок внешней касательной прямой.
Задача построения внутренней касательной прямой (рис. 33, б) решается, если вспомогательную окружность построить радиусом, равным R + R1,
§ 19. Сопряжение двух дуг окружностей третьей дугой
При построении сопряжения двух дуг окружностей третьей дугой заданного радиуса можно рассмотреть три случая: когда сопрягающая дуга радиуса R касается заданных дуг радиусов R1 и R2 с внешней стороны (рис. 34, а); когда она создает внутреннее касание (рис. 34, б); когда сочетаются внутреннее и внешнее касания (рис. 34, в).
Построение центра О сопрягающей дуги радиуса R при внешнем касании осуществляется в следующем порядке: из центра О1 радиусом, равным R + R1, проводят вспомогательную дугу, а из центра O2 проводят вспомогательную дугу радиусом R + R2. На пересечении дуг получают центр О сопрягаемой дуги радиуса R, а на пересечении радиусом R + R1и R + R2 с дугами окружностей получают точки сопряжения А и А1.
Построение центра О при внутреннем касании отличается тем, что из центра О1 проводят вспомогательную окружность радиусом, равным R — R1 а из центра О2 радиусом R — R2. При сочетании внутреннего и внешнего касания из центра О1 проводят вспомогательную окружность радиусом, равным R — R1, а из центра О2 — радиусом, равным R + R2.
§ 20. Сопряжение дуги окружности и прямой линии второй дугой
Здесь может быть рассмотрено два случая: внешнее сопряжение (рис. 35, а) и внутреннее (рис. 35, б). В том и в другом случае при построении сопрягающей дуги радиуса R центр сопряжения О лежит на пересечении геометрических мест точек, равно удаленных от прямой и дуги радиуса R на величину R1.
При построении внешнего сопряжения параллельно заданной прямой на расстоянии R1 в сторону окружности проводят вспомогательную прямую, а из центра О радиусом,равным R + R1,— вспомогательную окружность, и на их пересечении получают точку О1 — центр сопрягающей окружности. Из этого центра радиусом R проводят сопрягающую дугу между точками А и А1, построение которых видно из чертежа.

Рис. 34

Рис. 35
Построение внутреннего сопряжения отличается тем, что из центра О проводят вспомогательную дугу радиусом, равным R — R1.
§21. Овалы
Плавные выпуклые кривые, очерченные дугами окружностей разных радиусов, называют овалами. Овалы состоят из двух опорных окружностей с внутренними сопряжениями между ними.
Различают овалы трехцентровые и многоцентровые. При вычерчивании многих деталей, например кулачков, фланцев, крышек и других, контуры их очерчивают овалами. Рассмотрим пример построения овала по заданным осям. Пусть для четырехцентрового овала, очерченного двумя опорными дугами радиуса R и двумя сопрягающими дугами радиуса r , заданы большая ось АВ и малая ось CD. Величину радиусов R u r надо определить путем построений (рис. 36). Соединим концы большой и малой оси отрезком AС, на котором отложим разность СЕ большой и малой полуосей овала. Проведем перпендикуляр к середине отрезка AF, который пересечет большую и малую оси овала в точках О1 и О2. Эти точки будут центрами сопрягающихся дуг овала, а точка сопряжения будет лежать на самом перпендикуляре.

Рис. 36
§ 22. Лекальные кривые
Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, гиперболу, циклоиду, синусоиду эвольвенту и др.
Эллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее

Рис. 36

Рис. 37
точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности — прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.
Можно привести пример построения эллипса по двум сопряженным диаметрам (рис. 37,б) MN и KL. Сопряженными два диаметра называют, если каждый из них делит пополам хорды, параллельные другому диаметру. На сопряженных диаметрах строят параллелограмм. Один из диаметров MN делят на равные части; на такие же части делят и стороны параллелограмма, параллельные другому диаметру, нумеруя их, как показано на чертеже. Из концов второго сопряженного диаметра KL через точки деления проводят лучи. В пересечении одноименных лучей получают точки эллипса.
Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данной прямой — директрисы.
Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В (рис. 38, а). С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.
Можно привести пример построения параболы в виде кривой, касательной прямой с заданными на них точками А и В (рис. 38, б). Стороны угла, образованного этими прямыми, делят на равные части и ну-
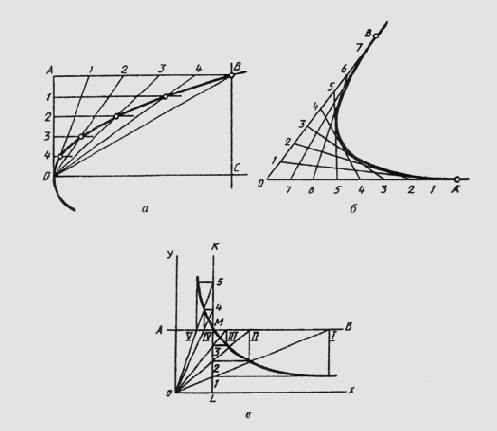
Рис. 38
меруют точки деления. Одноименные точки соединяют прямыми. Параболу вычерчивают как огибающую этих прямых.
Гиперболой называют плоскую незамкнутую кривую второго порядка, состоящую из двух веток, концы которых удаляются в бесконечность, стремясь к своим асимптотам. Гипербола отличается тем, что каждая точка ее обладает особым свойством: разность ее расстояний от двух данных точек-фокусов есть величина постоянная, равная расстоянию между вершинами кривой. Если асимптоты гиперболы взаимно перпендикулярны, она называется равнобокой. Равнобокая гипербола широко применяется для построения различных диаграмм, когда задана своими координатами одна точка М (рис. 38, в). В этом случае через заданную точку проводят линии АВ и KL параллельно координатным осям. Из полученных точек пересечения проводят линии, параллельные координатным осям. В их пересечении получают точки гиперболы.
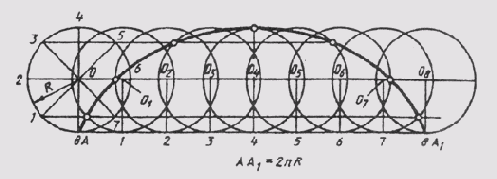
Рис. 39
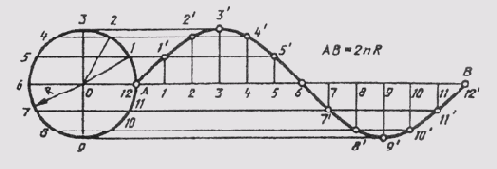
Рис. 40
Циклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности (рис. 39). Для построения циклоиды от исходного положения точки А откладывают отрезок АА], отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О1, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.
Синусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды (рис. 40) нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.
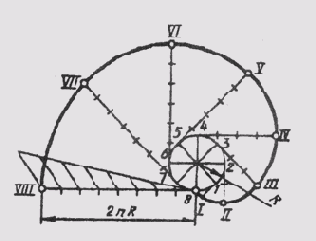
Рис. 41
Эвольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис. 41): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей.На первой касательной откладывают одно деление 2лR/n , на второй — два и т. д.
Полученные точки соединяют плавной кривой и получают эвольвенту окружности.
§ 23. Определение чертежа
Чертежом называют графический документ, содержащий изображения предметов (деталей, узлов, машин, зданий и сооружений и т. д.), выполненных с учетом правил и требований, позволяющих однозначно различать эти предметы. Таким образом, процесс выполнения чертежей основан на знании специальных законов и умении использовать их при выполнении графических работ. Теоретической основой черчения является наука о методах изображения геометрических фигур на плоскости — начертательная геометрия.
К чертежам предъявляют ряд общих требований. Так, чертеж должен быть наглядным и давать четкое представление об изображаемом предмете. Чертеж должен быть обратимым. Это необходимо, чтобы по нему можно было точно воспроизвести форму и размеры изображаемого предмета. Чертеж должен быть простым для графического исполнения и др.
Надо также отметить, что знание графических законов способствует развитию пространственного мышления, являющегося основой технического творчества проектировщиков, конструкторов, изобретателей и рационализаторов.
§ 24. Основные элементы геометрического пространства
В инженерной графике геометрическое пространство рассматривается как множество однородных элементов. К основным формообразующим элементам геометрического пространства относятся точки, линии (прямые и кривые), поверхности (плоские и кривые).

Рис. 42
Различают пространство евклидово и неевклидово. Евклидово пространство характеризуется тем, что расположенные в нем параллельные прямые линии или плоскости не пересекаются. Характеристики евклидова пространства не учитывают ряда других геометрических свойств пространства. В более широком понимании эти свойства учитывают проективное пространство, в котором параллельные между собой прямые (плоскости) пересекаются. Эти пересечения происходят в так называемой несобственной точке, которая расположена в бесконечности проективного пространства. Для примера можно привести две параллельные плоскости S и S1 (рис. 42). Проведем в плоскости S прямую К, а в плоскости Si прямую L так, чтобы они были параллельны. В проективном пространстве эти прямые пересекаются вне собственной точки Ебесконечность. Далее в плоскости S проведем прямую т, а в плоскости Si прямую п так, чтобы они были параллельны. Эти прямые также пересекутся вне собственной точки F бесконечность. Нетрудно видеть, что несобственные точки Е бесконечность и F бесконечность определяют несобственную прямую d бесконечность . Учитывая, что несобственные точки принадлежат и плоскости S, и плоскости S1, можно утверждать, что несобственная прямая также принадлежит этим плоскостям. Таким образом, мы имеем случай, когда две параллельные плоскости S и S1пересекаются по бесконечно удаленной несобственной прямой d бесконечность.
Характеристики проективного пространства позволяют в ряде случаев упростить формулировки, принятые для евклидова пространства. Это можно подтвердить следующим примером. В аксиомах евклидова пространства отмечается, что две прямые определяют единственную точку, если они не параллельны. Для проективного пространства оговорка «если они не параллельны» теряет смысл.
В общепринятом смысле пространство можно рассматривать как бесконечное. Однако геометрическое пространство может быть рассмотрено с позиций размерности. Так, множество положений точки, перемещающейся в заданном прямолинейном направлении, образует бесконечную прямую линию, представляющую собой одномерное пространство. Если же прямую перемещать в заданном направлении, не параллельном самой прямой, она образует бесконечную поверхность (в данном случае плоскость), представляющую собой двухмерное пространство. Задав плоскости (поверхности) направление, не параллельное ей и перемещая ее в этом направлении, получим трехмерное пространство. Таким же путем можно получить четырехмерное и в общем виде многомерное пространство.
Примем следующие обозначения элементов пространства. Точки будем обозначать прописными буквами латинского алфавита: А, В, С... или цифрами 1, 2, 3...; прямые — строчными буквами латинского алфавита: а, b, с..., а плоскости — прописными буквами греческого алфавита: Г, Л, П, S, Ф, ¥, Q.
Между элементами пространства существуют следующие отношения.
Тояадественность обозначается знаком ==, например А == В. Это обозначает, что точка А совпадает с точкой В.
Инцидентность (или принадлежность) обозначается знаком €. Например, А € а обозначает, что точка А принадлежит (инцидентна) прямой а.
Параллельность обозначается знаком ||. Например, K || L обозначает, что прямая К параллельна прямой
Перпендикулярность обозначается знаком _|_. Например, a _|_ S обозначает, что прямая а перпендикулярна плоскости S.
Над элементами пространства можно выполнить операцию соединение, которую обозначают знаком и. Например, запись А и В ~ а обозначает, что в результате соединения точек А и В получена прямая а. Операцию пересечение обозначают знаком ^. Запись т ^ n = К обозначает, что в результате пересечения прямых тип получена точка К.
§ 25. Геометрические тела и их отображение
Геометрическое тело рассматривают как множество всех принадлежащих ему точек, связанных между собой и ограниченных в пространстве соответствующим образом. Оно может перемещаться в пространстве без изменения взаимного положения его элементов.
В инженерной графике рассматриваются одномерные тела (отрезок линии), двухмерные (плоская фигура, отсек поверхности), трехмерные (любая объемная фигура). Основными предметами изображения на плоских чертежах являются трехмерные геометрические тела, окружающие нас в реальном трехмерном пространстве.
Сложные геометрические тела можно рассматривать и как состоящие из более простых трехмерных фигур, которые определяются основными формообразующими элементами пространства — точками, линиями, поверхностями.
Геометрические тела на чертежах получают методом отображения. Отображение геометрического тела — это понятие, в соответствии с которым каждой точке трехмерного пространства соответствует конкретная точка двухмерного пространства на чертеже. Отображение геометрических тел может быть выполнено на плоскость или какую-либо другую поверхность. В курсе инженерной графики рассматривается отображение геометрических тел на плоскость. Изображение геометрического тела на плоскости можно получить путем проецирования ее точек на эту плоскость.
Геометрическая связь между геометрическим телом, расположенным в пространстве, и его отображением на чертеже на плоскости устанавливаются по законам проецирования, которые базируются на принципе взаимно-однозначного соответствия.
§ 26. Метод проекций
Теоретические свойства построения чертежа в инженерной графике базируются на правилах построения изображений, основанных на методе проекций. Изображение объектов трехмерного пространства на плоскости получают методом проецирования. Проецирование — это процесс, в результате которого получают изображения, представляющие собой проекции на плоскости.
Аппарат проецирования включает в себя изображаемые объекты — точки А, В, проецирующие лучи i и плоскость проекции п', на которой получается изображение объектов (рис. 43). Процесс проецирования заключается в проведении проецирующих лучей через заданные точки до встречи с плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций и определяет проекцию этой точки. Так, проекцией точки А является точка А', т. е. [i ~ A; i ^ п' = А']. Проекцией точки В является точка В', хотя проекция точки В, лежащей в плоскости п', совпала с самой точкой. Чтобы получить проекцию какой-либо фигуры, необходимо построить проекции ее характерных точек и соединить их на чертеже соответствующими линиями.
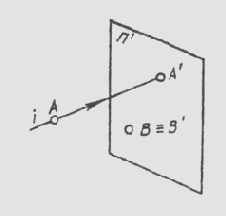
Рис. 43
§ 27. Способы проецирования
Построить проекции предметов на чертеже можно двумя способами: центральным и параллельным.
Сущность центрального способа проецирования заключается в том, что все лучи, проецирующие предмет, исходят из одной точки Р, называемой центром проекций (рис. 44). Полученные проекции А', В', С' называются центральными проекциями точек А, В, С.
Сущность параллельного способа заключается в том, что все проецирующие лучи проходят параллельно наперед заданному направлению 5, а значит и друг другу (рис. 45). Это можно уподобить случаю центрального способа проецирования, когда центр проекций S удален в бесконечность и все проецирующие лучи становятся параллельны-
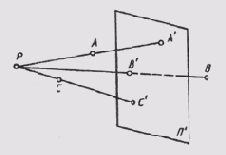
Рис. 44
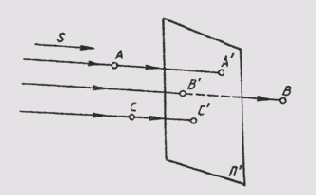
Рис. 45
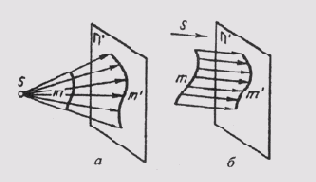
Рис. 46
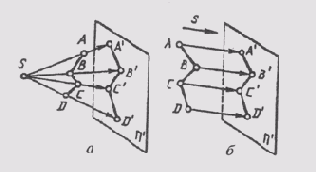
Рис. 47
ми. При построении проекций А', В', С' этим способом они называются параллельными проекциями точек А, В, С.
При проецировании совокупность проецирующих лучей образует различные геометрические фигуры. При проецировании прямой линии — это плоскость (рис. 46) при проецировании ломаной линии — поверхность призмы или пирамиды (рис. 47), при проецировании кривой линии — коническая или цилиндрическая поверхность (рис. 48). В отличие от проецируемых фигур эти фигуры называют проецирующими.
§ 28. Свойства проекций
Проекции, полученные при центральном и параллельном проецировании, обладают рядом свойств.
Проекция точки есть точка. При заданном центре Р (.или направлении S) проецированию любой точки А пространства соответствует иа плоскости проекций п' единственная точка А'. При этом проекция точки В, лежащей в плоскости проекций, совпадает с самой точкой (см. рис. 43).
Проекция прямой есть прямая. На рис. 46 лучи, проецирующие прямую т, создают плоскость S, которая пересекает плоскость проекций п' по линии m', являющейся проекцией на плоскость n'; S ~ т; S п п = т'. Проекция прямой определена, если известны проекции хотя бы двух ее точек (рис. 49). Если в пространстве прямая параллельна плоскости проекции п', то ее проекция параллельна самой прямой (рис. 50). При этом при центральном проецировании проекции отрезков пропорциональны самим отрезкам, а при параллельном — равны им.
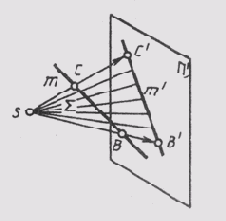
Рис. 49
При параллельном проецировании сохраняется отношение величин отрезков прямой и их проекций (рис. 51):
АВ/ВС = А'В'/В'С.
При параллельном проецировании проекции параллельных прямых есть прямые параллельные (рис. 52). Если прямые т и п в пространстве параллельны, то и проецирующие их плоскости Sm и Sn тоже будут параллельны. При пересечении их с плоскостью проекций п' получаем т'|| п'.
Проекцией плоскости является плоскость проекций. Плоскость состоит из бесконечного множества точек. При проецировании этого множества проецирующие лучи заполняют все пространство, а
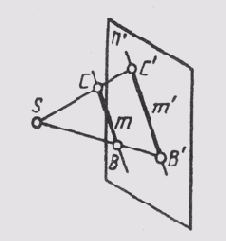
Рис. 50

Рис. 51
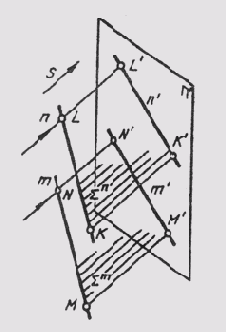
Рис. 52
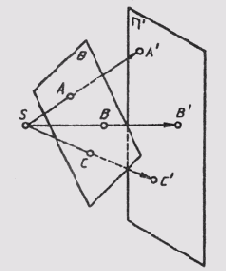
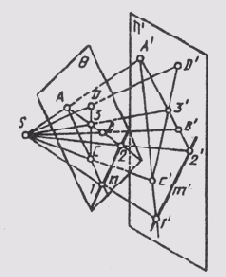
Рис. 53
их точки пересечения с плоскостью проекций п' — всю плоскость проекций.
Так как положение любой плоскости в пространстве определяется тремя ее точками, не лежащими на одной прямой, то проекция трех таких точек плоскости (рис. 53, а) устанавливает однозначное соответствие между проецирующей плоскостью и плоскостью проекций n', которое позволяет определить проекции (рис. 53, б) любой точки D или прямой этой плоскости.
Если плоскость параллельна плоскости проекций, то проекции ее плоских фигур при центральном проецировании подобны самим фигурам (рис. 54, а), а при параллельном — равны им (рис. 54,6).
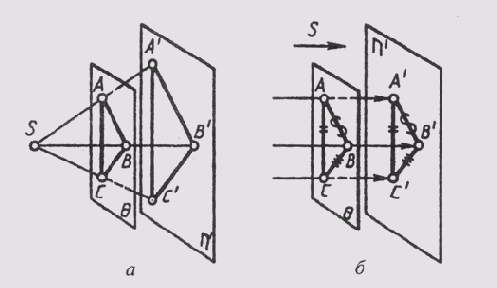
Рис. 54
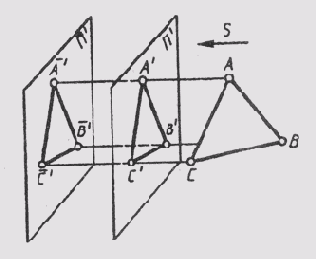
Рис. 55
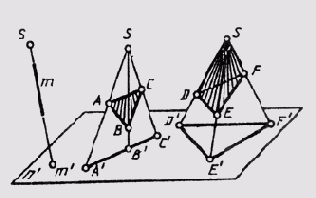
Рис. 56
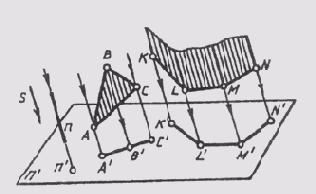
Рис. 57
Если плоскость угла параллельна плоскости проекций, величина проекции угла и при центральном, и при параллельном проецировании равна натуральной величине. На рис. 54, a угол ABC = уголA'B'C', так как АВС бесконечность А'В'С', а на рис. 54, б угол ABC = углу А'В'С', так как АВС = А'В'С'.
При параллельном проецировании проекции фигуры не изменяется при параллельном переносе плоскости j проекций (рис. 55).
Прямые и плоскости (поверхности) могут занимать в пространстве проецирующее положение, если с ними совпадают проецирующие лучи. При центральном проецировании это прямые и плоскости, проходящие через центр проекций, пирамидальные и конические поверхности, у которых вершины совпадают с центром проецирования (рис. 56). При параллельном проецировании — это прямые и плоскости, параллельные направлению проецирования, призматические и цилиндрические поверхности, ребра и образующие которых параллельны направлению проецирования (рис. 57).
Все эти геометрические фигуры можно рассматривать состоящими из проецирующих лучей, каждый из которых изображается точкой. Отсюда следует, что проекциями прямых, плоскостей, поверхностей, занимающих проецирующее положение, есть точки или линии их пересечения с плоскостью проекций («вырожденные» проекции).
§ 29. Ортогональные проекции
Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций. Ортогональным проекциям присущи все свойства параллельных проекций, но при прямоугольном проецировании проекция отрезка, если он не параллелен плоскости проекций, всегда меньше самого отрезка (рис. 58). Это объясняется тем, что сам отрезок в пространстве является гипотенузой прямоугольного треугольника, а его проекция — катетом: А'В' = ABcos a.
При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.
Теорема о проецировании прямого угла. Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпенди-
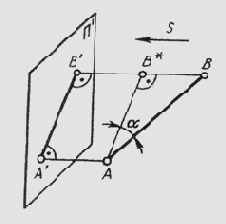
Рис. 58
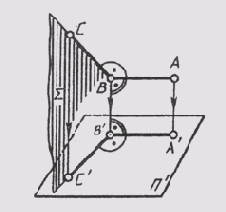
Рис. 59
кулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой же угол.
Пусть дан прямой угол ABC, у которого сторона АВ параллельна плоскости п' (рис. 59). Проецирующая плоскость перпендикулярна плоскости п'. Значит, АВ _|_S, так как АВ _|_ ВС и АВ _|_ ВВ, отсюда АВ _|_ В'С'. Но так какАВ || А'В' _|_ В'С', т. е. на плоскости п' угол между А'В' и В'С равен 90°.
Обратимость чертежа. Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А (см. рис. 53) не определяет положение самой точки в пространстве, так как не известно, на какое расстояние она удалена от плоскости проекций п'. Любая точка проецирующего луча, проходящего через точку А, будет иметь своей проекцией точку А'. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображение дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа. В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексные чертежи) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрические чертежи).
§ 30. Аксонометрические проекции
В ряде случаев для пояснения прямоугольных проекций сложных деталей, машин и механизмов применяют аксонометрические проекции. С их помощью получают наглядное изображение предметов. Сущность аксонометрического проектирования заключается в том, что фигуру, связанную с пространственной системой координатных осей, вместе с этими осями координат проецируют на одну плоскость, называемую плоскостью аксонометрических проекций. Подробно аксонометрические проекции рассмотрены в гл. 12.
§31. Проекции с числовыми отметками
Сущность метода проекций с числовыми отметками заключается в том, что любая точка пространства проецируется ортогонально на одну горизонтальную плоскость, называемую плоскостью нулевого уровня. Положение точки по отношению к этой плоскости определяется числовой отметкой, проставляемой у буквенного обозначения проекции точки и представляющую собой число единиц расстояния от точки до плоскости проекций.
§ 32. Комплексный чертеж точки
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. Проекции элементов
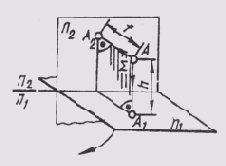
Рис. 60
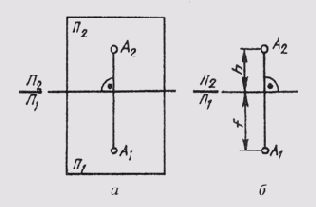
Рис. 61
пространства на ней будем обозначать с индексом 1 : А1, а1, S1 ... и называть горизонтальными проекциями (точки, прямой, плоскости).
Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П2. Проекции элементов пространства на ней будем обозначать с индексом 2: А2, <a2, S2 и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.
Спроецируем точку А ортогонально на обе плоскости проекций:
АА1_|_ П1;AА1 ^П1=A1;
АА2_|_ П2;AА2 ^П2=A2;
Проецирующие лучи АА1 и АА2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1 с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1.
Прямая А1А2, соединяющая горизонтальную А1 и фронтальную А2 проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.
§ 33. Элементы трехпроекционного комплексного чертежа точки
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-

Рис. 62
ной. Фронтальная и профильная проекции точки всегда лежат на одной горизонтальной линии связи. Причем A1A2 _|_ А2А1 и А2А3, _|_ П2/П3.
Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроек-ционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-

Рис. 63
ется, проекции точек могут быть даны без изображения осей (рис. 63, а, б). Такая система называется безосновой. Линии связи могут также проводиться с разрывом (рис. 63, б).
§ 34. Положение точки в пространстве трехмерного угла
Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи:
точка расположена в пространстве (см. рис. 62). В этом случае она имеет глубину, высоту и широту;
точка расположена на плоскости проекций П1 — она не имеет высоты, П2 — не имеет глубины, Пз — не имеет широты;
точка расположена на оси проекций, П2/П1 не имеет глубины и высоты, П2/П3— не имеет глубины и широты и П1/П3не имеет высоты и широты.
§ 35. Конкурирующие точки
Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П1 [А1 == В1]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости
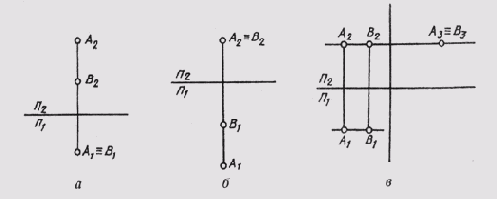
Рис. 64
П2 (рис. 64, б), они называются фронтально конкурирующими. И если проекции точек А и В совпадают на плоскости П3 [А3 == B3] (рис. 64, в), они называются профильно конкурирующими.
По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.
§ 36. Замена плоскостей проекций
Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных.
На рис. 65, а показаны точка А и ее проекции — горизонтальная А1 и фронтальная А2. По условиям задачи необходимо произвести замену плоскостей П2. Новую плоскость проекции обозначим П4 и расположим перпендикулярно П1. На пересечении плоскостей П1 и П4 получим новую ось П1/П4. Новая проекция точки А4 будет расположена на линии связи, проходящей через точку А1 и перпендикулярно оси П1/П4.
Поскольку новая плоскость П4 заменяет фронтальную плоскость проекции П2, высота точки А изображается одинаково в натуральную величину и на плоскости П2, и на плоскости П4.
Это обстоятельство позволяет определить положение проекции A4, в системе плоскостей П1 _|_ П4 (рис. 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-
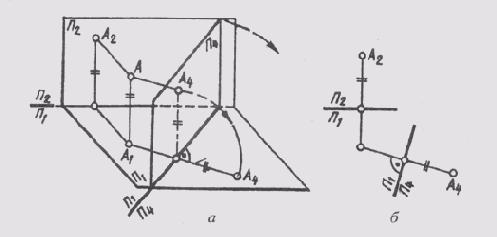
Рис. 65
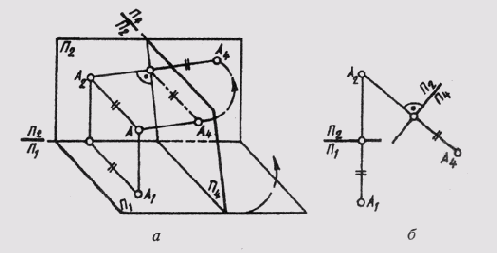
Рис. 66
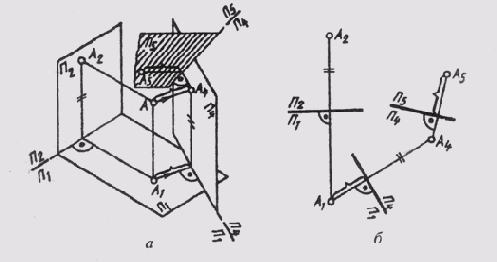
Рис. 67
сти проекции П2, отложить ее на новой линии связи от новой оси проекций — и новая проекция точки А4 будет построена.
Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П4 _|_ П2 (рис. 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А2А4 _|_. В этом случае глубина точки одинакова и на плоскости П1, и на плоскости П4. На этом основании строят А4 (рис. 66, б) на линии связи А2А4 на таком расстоянии от новой оси П1/П4 на каком А1 находится от оси П2/П1.
Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П5. Ее располагают перпендикулярно уже введенной плоскости П4 (рис. 67, а), т. е. П5П4 и производят построение, аналогичное ранее рассмотренным. Теперь расстояния измеряют на заменяемой второй из основных плоскостей проекций (на рис. 67, б на плоскости П1) и откладывают их на новой линии связи А4А5, от новой оси проекций П5/П4. В новой системе плоскостей П4П5 получают новый двухпроекционный чертеж, состоящий из ортогональных проекций А4 и А5, связанных линией связи
A4A5_|_П4/П5
§ 37. Прямоугольные координаты точек
Три основные плоскости проекций (П1_|_П2 _|_ П3) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у,П2/П3 —осью аппликат z.
Начало координат (точка О) располагается в точке пересечения осей координат (рис. 68, а).
Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А1 ортогонально проецировать на ось х в точку Ах. Тогда получим пространственную координатную ломаную АА1АХО, отрезки которой параллельны осям координат и соответственно называются: ОАХ — отрезком абсциссы; АХ А1 — отрезком ординат; А1А — отрезком аппликаты.
Измерив координатные отрезки единицей длины l, получим три отвлеченных числа — три координаты точки А:
х = OAX абсцисса; у = AxA1— ордината; z = AA1 — аппликата.
Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение
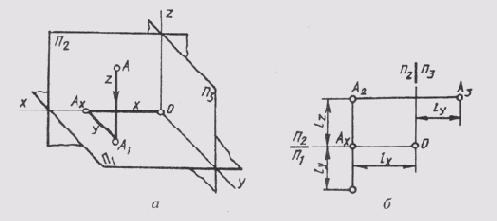
Рис. 68
вертикальной линии связи (рис. 68, б). Горизонтальная проекция точки определяется величиной ординаты, а фронтальная — величиной аппликаты.
§ 21,22, Поэтому приведем
Окружность — плоская кривая второго порядка, ортогональная проекция которой может быть окружностью и эллипсом (рис. 81, а). Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров. Удобнее всего строить проекции диаметров, параллельных плоскостям проекций: АВ || П1 CD || П2; CD _|_ П1 (рис. 81, б). Фронтальная проекция окружности — эллипс — определяется малой осью эллипса A1B2 = dcos b и большой осью эллипса С2D2=d

Рис. 79

Рис. 80

Рис. 81
Если плоскость окружности наклонена ко всем основным плоскостям проекций, то все три ее проекции есть эллипсы, которые можно построить по сопряженным диаметрам, являющимся проекциями тех диаметров окружности, которые параллельны плоскостям проекций (см. рис. 37).
Цилиндрическая винтовая линия (гелиса) — пространственная кривая, представляющая собой траекторию точки, выполняющей винтовое движение. Винтовое движение включает в себя равномерное поступательное движение точки по прямой и равномерное вращательное движение этой прямой с точкой вокруг оси i, которой прямая параллельна. Высота p, на которую точка поднимается по прямой за полный оборот, называется шагом винтовой линии (рис. 82). Если ось i винтовой линии перпендикулярна горизонтальной плоскости проекций, то горизонтальная проекция винтовой линии есть окружность, а фронтальная — синусоида.
Для построения фронтальной проекции винтовой линии при заданном диаметре d и шаге р нужно разделить и окружность, и шаг на равное число частей. Построение проекций точки винтовой линии показано на рис. 82. Цилиндрическую винтовую линию можно развер-

Рис. 82
нуть на плоскость. Развертка ее представляет собой прямую линию с углом подъема а, где tga = P / лd.
§ 28); Это означает, что
На комплексном чертеже кривой ее особые точки, к которым относятся точки перегиба, возврата, излома, узловые точки, являются особыми точками и на ее проекции. Это объясняется тем, что особые точки кривых связаны с касательными в этих точках.
Если плоскость кривой занимает проецирующее положение (рис. 80, а), то одна проекция этой кривой имеет форму прямой. У пространственной кривой все ее проекции — кривые линии (рис. 80, б).
Чтобы установить по чертежу, какая задана кривая (плоская или пространственная), необходимо выяснить, принадлежат ли все точки кривой одной плоскости. Заданная на рис. 80, б кривая является пространственной, так как точка D кривой не принадлежит плоскости, определяемой тремя другими точками А, В и Е этой кривой.
Построение и изображение кривых рассматривалось в
§ 38. Образование линий
В общем случае линию можно представить как множество последовательных положений перемещающейся в пространстве точки. Если точка передвигается без изменения направления, образуется прямая линия, если направление движения точки меняется — образуется кривая линия.
Если точка перемещается в одной плоскости, образуется плоская линия, если ее траектория выходит за пределы одной плоскости — такую линию называют пространственной. Пространственные линии не лежат всеми своими точками в одной плоскости. Их называют также линиями двоякой кривизны.
Примерами плоских линий могут быть окружность, эллипс, овал. В качестве примера пространственной линии можно привести винтовую линию.
Плоские линии делят на циркульные, состоящие из сопряженных дуг окружностей, и лекальные — имеющие переменную кривизну. На чертежах циркульные линии проводятся с помощью циркуля, а лекальные — с помощью лекал.
Графически на чертеже линии задаются с помощью проекций. При этом должна быть показана проекционная связь хотя бы одной ее точки, что позволяет избежать неопределенности.
Простейшим видом линии является прямая.
§ 39. Комплексный чертеж прямой линии
Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.
На рис. 69, а показаны прямая l и принадлежащие ей точки А и В. Для построения фронтальной проекции прямой l2 достаточно построить фронтальные проекции точек А2 и В2 и соединить их прямой. Аналогично строится горизонтальная проекция, проходящая через горизонтальные проекции точек А1 и В1. После совмещения плоскости П1 с плоскостью П2 получим двухпроекционный комплексный чертеж прямой l (рис. 69, б).
Профильную проекцию прямой можно построить с помощью профильных проекций точек А и В. Кроме того, профильную проекцию прямой можно построить, используя разность расстояний двух ее точек до фронтальной плоскости проекций, т. е. разность глубин точек (рис. 69, в). В этом случае отпадает необходимость наносить оси проекций на чертеж. Этот способ, как более точный, и используется в практике выполнения технических чертежей.
§ 40. Расположение прямой относительно плоскостей проекций
Относительно плоскостей проекций прямая может занимать различное положение. Прямую, не параллельную ни одной из основных плоскостей проекций (см. рис. 69), называют прямой общего положения. Прямую, параллельную или перпендикулярную одной из плоскостей проекций, называют прямой частного положения.
Прямые, параллельные одной из плоскостей проекций, называют прямыми уровня. Название их зависит от того, какой плоскости они параллельны. Прямую, параллельную горизонтальной плоскости проекций, называют горизонталью и обозначают на чертежах h (рис. 70).
Прямую, параллельную фронтальной плоскости проекций, называют фронталью и обозначают f (рис.71).

Рис. 69

Рис. 70

Рис. 71

Рис. 72
Прямую, параллельную профильной плоскости проекций, называют профильной и обозначают р (рис. 72).
У прямой уровня одна проекция параллельна самой прямой и определяет углы наклона этой прямой к двум другим плоскостям проекций.
Параллельность одной из плоскостей проекций определяет расположение двух других проекций прямой уровня:
h2 || П2/П1 ;
h3 _|_ П2/П3 ;
f2 || П2/П1;
f3 _|_ П2/П3 ;
p1 _|_ П2/П1 ;
p2 _|_ П2/П1 ;
Прямые h2 и f1 перпендикулярны вертикальным линиям связи; р1 и р2 располагаются на одной вертикальной линии связи и при двухпроекционном чертеже должны быть определены двумя точками прямой р.
Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых одна проекция превращается в точку, а две другие проекции параллельны самой

Рис. 73
прямой и совпадают на чертеже с направлением линии связи (рис. 73). Различают горизонтально проецирующие прямые (АВ), фронтально проецирующие прямые (CD) и профильно проецирующие прямые (EF).
§ 41. Взаимное расположение двух прямых
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а = b, быть параллельными c|| d, пересекаться т ^ n и скрещиваться (k° / l).
Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):
m^n=M->{m1^n1=M1 или m2^n2= М2}
Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):

Рис. 74
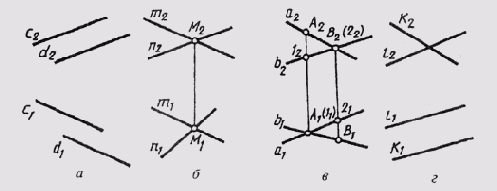
Рис. 75
a°/b —> а1 ^ b1 = А1(l1) — горизонтально конкурирующие точки; а2^b1 = В2(l1) — фронтально конкурирующие точки. В другом случае одна пара проекций будет пересекаться, а вторая может быть параллельными прямыми (рис. 75, г):
k0 /l ->{ k2 ^ l2 или k1 || l1}
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, б) окажутся профильными прямыми, то для определения их взаимного расположения необходимо построить третью, профильную проекцию этих прямых. Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.
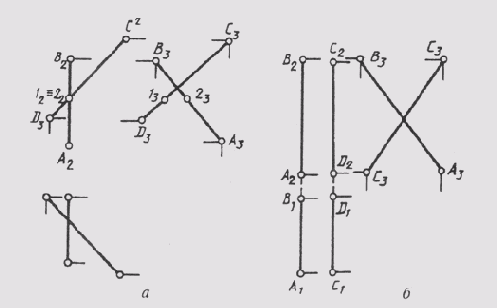
Рис. 76
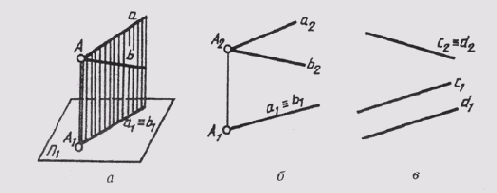
Рис. 77
Рассматривая рис. 76, б можно ошибочно предположить, что прямые АВ и CD параллельны. Но после построения их профильных проекций увидим, что они скрещиваются, так как на этой плоскости проекции их пересекаются.
Две прямые, параллельные или пересекающиеся, могут иметь общую проецирующую плоскость (рис. 77, а). Тогда их изображения на соответствующую плоскость проекций совпадут. Такие прямые называют конкурирующими:
a^b=A->{а2 ^b2=А2 или а1==b1 ,A1~а1(b1)}
Прямые а и b горизонтально конкурирующие, имеют общую горизонтально проецирующую плоскость (рис. 77, б). Прямые с и d (рис. 77, в) — фронтально конкурирующие, имеют общую фронтально проецирующую плоскость.
§ 42. Определение натуральной величины отрезка прямой линии
При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.
Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см. рис. 69).
Возьмем отрезок общего положения АВ (A ^ П1) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А1ВВ1, в котором гипотенузой является сам отрезок, одним катетом — горизонтальная проекция этого отрезка, а вторым катетом — разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.
Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П1.

Рис. 78
Для определения натуральной величины отрезка прямой можно воспользоваться поворотом ее относительно плоскостей проекций, чтобы она расположилась параллельно одной из них (см.
§ 43. Кривые линии
Кривые линии на комплексном чертеже задают своими проекциями, которые строят по проекциям отдельных точек, принадлежащих этой линии. Проекции линий при ортогональном проецировании получают как результат пересечения проецирующих цилиндров с плоскостями проекций (см.
§ 44. Взаимное расположение точки и линии
Точка в пространстве по отношению к линии может занимать два положения: принадлежать ей или не принадлежать. Если она принадлежит линии, она составляет с ней единое целое и проекции ее на чертеже лежат на соответствующих проекциях линии, а также на одной линии связи.
Если же хотя бы одна из проекций точки не лежит на проекции линии, точка ей не принадлежит. На рис. 83 показан комплексный чертеж линии l, а также ряда точек. Из чертежа видно, что точка А принадлежит линии b, так как горизонтальная ее проекция А1 лежит на горизонтальной проекции линии 11, а фронтальная проекция точки А2 расположена на фронтальной проекции прямой А и ле-
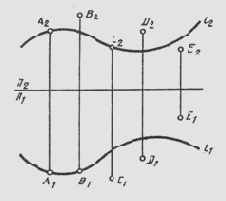
Рис. 83
жит на одной вертикальной линии связи с точкой А1. Точки В и С не принадлежат линии l, так как в первой фронтальная, а во второй горизонтальная проекции не принадлежат соответствующим проекциям линии. Точки D и Е не принадлежат линии l, так как ни одна из их проекций не принадлежит соответствующей проекции линии.
