§ 32. Комплексный чертеж точки
Чтобы построить изображение предмета, сначала изображают отдельные его элементы в виде простейших элементов пространства. Так, изображая геометрическое тело, следует построить его вершины, представленные точками; ребра, представленные прямыми и кривыми линиями; грани, представленные плоскостями и т.д
Правила построения изображений на чертежах в инженерной графике основываются на методе проекций. Одно изображение (проекция) геометрического тела не позволяет судить о его геометрической форме или форме простейших геометрических образов, составляющих это изображение. Таким образом, нельзя судить о положении точки в пространстве по одной ее проекции; положение ее в пространстве определяется двумя проекциями.
Рассмотрим пример построения проекции точки А, расположенной в пространстве двугранного угла (рис. 60). Одну из плоскостей проекции расположим горизонтально, назовем ее горизонтальной плоскостью проекций и обозначим буквой П1. Проекции элементов
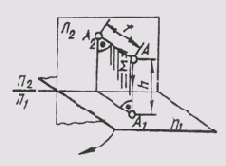
Рис. 60
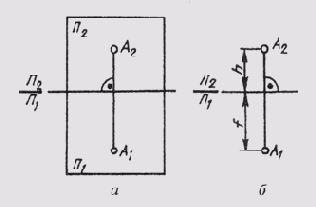
Рис.
61
Вторую плоскость расположим вертикально перед наблюдателем, перпендикулярно первой, назовем ее вертикальной плоскостью проекций и обозначим П2. Проекции элементов пространства на ней будем обозначать с индексом 2: А2, <a2, S2 и называть фронтальными проекциями (точки, прямой, плоскости). Линию пересечения плоскостей проекций назовем осью проекций.
Спроецируем точку А ортогонально на обе плоскости проекций:
АА1_|_ П1;AА1 ^П1=A1; АА2_|_ П2;AА2 ^П2=A2;
Проецирующие лучи АА1 и АА2 взаимно перпендикулярны и создают в пространстве проецирующую плоскость АА1АА2, перпендикулярную обеим сторонам проекций. Эта плоскость пересекает плоскости проекций по линиям, проходящим через проекции точки А.
Чтобы получить плоский чертеж, совместим горизонтальную плоскость проекций П1 с фронтальной плоскостью П2 вращением вокруг оси П2/П1 (рис. 61, а). Тогда обе проекции точки окажутся на одной линии, перпендикулярной оси П2/П1. Прямая А1А2, соединяющая горизонтальную А1 и фронтальную А2 проекции точки, называется вертикальной линией связи.
Полученный плоский чертеж называется комплексным чертежом. Он представляет собой изображение предмета на нескольких совмещенных плоскостях. Комплексный чертеж, состоящий из двух ортогональных проекций, связанных между собой, называется двухпроекционным. На этом чертеже горизонтальная и фронтальная проекции точки всегда лежат на одной вертикальной линии связи.
Две связанные между собой ортогональные проекции точки однозначно определяют ее положение относительно плоскостей проекций. Если определить положение точки а относительно этих плоскостей (рис. 61, б) ее высотой h (АА1 =h) и глубиной f(AA2 =f), то эти величины на комплексном чертеже существуют как отрезки вертикальной линии связи. Это обстоятельство позволяет легко реконструировать чертеж, т. е. определить по чертежу положение точки относительно плоскостей проекций. Для этого достаточно в точке А2 чертежа восстановить перпендикуляр к плоскости чертежа (считая ее фронтальной) длиной, равной глубине f. Конец этого перпендикуляра определит положение точки А относительно плоскости чертежа.
§ 33. Элементы трехпроекционного комплексного чертежа точки
Для определения положения геометрического тела в пространстве и получения дополнительных сведений на их изображениях может возникнуть необходимость в построении третьей проекции. Тогда третью плоскость проекций располагают справа от наблюдателя перпендикулярно одновременно горизонтальной плоскости проекций П1 и фронтальной плоскости проекций П2 (рис. 62, а). В результате пересечения фронтальной П2 и профильной П3 плоскостей проекций получаем новую ось П2/П3, которая располагается на комплексном чертеже параллельно вертикальной линии связи A1A2 (рис. 62, б). Третья проекция точки А — профильная — оказывается связанной с фронтальной проекцией А2 новой линией связи, которую называют горизонталь-
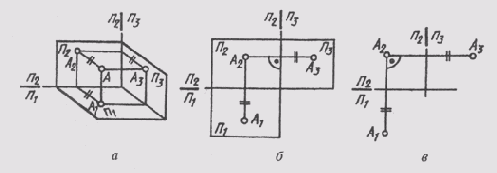
Рис.
62
Положение точки в пространстве в этом случае характеризуется ее широтой — расстоянием от нее до профильной плоскости проекций П3, которое обозначим буквой р.
Полученный комплексный чертеж точки называется трехпроек-ционным.
В трехпроекционном чертеже глубина точки АА2 проецируется без искажений на плоскости П1и П2 (рис. 62, а). Это обстоятельство позволяет построить третью — фронтальную проекцию точки А по ее горизонтальной А1 и фронтальной А2 проекциям (рис. 62, в). Для этого через фронтальную проекцию точки нужно провести горизонтальную линию связи A2A3 _|_A2A1. Затем в любом месте на чертеже провести ось проекций П2/П3 _|_ А2А3, измерить глубину f точки на горизонтальном поле проекции и отложить ее по горизонтальной линии связи от оси проекций П2/П3. Получим профильную проекцию А3 точки А.
Таким образом, на комплексном чертеже, состоящем из трех ортогональных проекций точки, две проекции находятся на одной линии связи; линии связи перпендикулярны соответствующим осям проекций; две проекции точки вполне определяют положение ее третьей проекции.
Необходимо отметить, что на комплексных чертежах, как правило, не ограничивают плоскости проекций и положение их задают осями (рис. 62, в). В тех случаях, когда условиями задачи этого не требу-
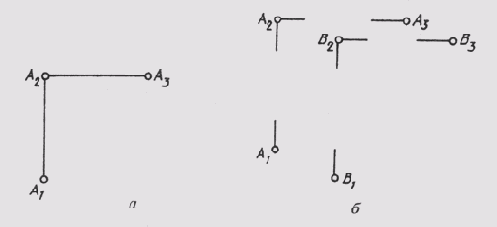
Рис.
63
§ 34. Положение точки в пространстве трехмерного угла
Расположение проекций точек на комплексном чертеже зависит от положения точки в пространстве трехмерного угла. Рассмотрим некоторые случаи: точка расположена в пространстве (см. рис. 62). В этом случае она имеет глубину, высоту и широту;
точка расположена на плоскости проекций П1 — она не имеет высоты, П2 — не имеет глубины, Пз — не имеет широты;
точка расположена на оси проекций, П2/П1 не имеет глубины и высоты, П2/П3— не имеет глубины и широты и П1/П3не имеет высоты и широты.
§ 35. Конкурирующие точки
Две точки в пространстве могут быть расположены по-разному. В отдельном случае они могут быть расположены так, что проекции их на какой-нибудь плоскости проекций совпадают. Такие точки называются конкурирующими. На рис. 64, а приведен комплексный чертеж точек А и В. Они расположены так, что проекции их совпадают на плоскости П1 [А1 == В1]. Такие точки называются горизонтально конкурирующими. Если проекции точек A и В совпадают на плоскости
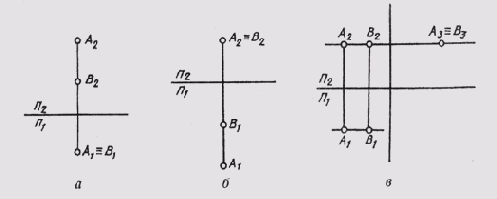
Рис.
64
По конкурирующим точкам определяют видимость на чертеже. У горизонтально конкурирующих точек будет видима та, у которой больше высота, у фронтально конкурирующих — та, у которой больше глубина, и у профильно конкурирующих — та, у которой больше широта.
§ 36. Замена плоскостей проекций
Свойства трехпроекционного чертежа точки позволяют по горизонтальной и фронтальной ее проекциям строить третью на другие плоскости проекций, введенные взамен заданных.
На рис. 65, а показаны точка А и ее проекции — горизонтальная А1 и фронтальная А2. По условиям задачи необходимо произвести замену плоскостей П2. Новую плоскость проекции обозначим П4 и расположим перпендикулярно П1. На пересечении плоскостей П1 и П4 получим новую ось П1/П4. Новая проекция точки А4 будет расположена на линии связи, проходящей через точку А1 и перпендикулярно оси П1/П4.
Поскольку новая плоскость П4 заменяет фронтальную плоскость проекции П2, высота точки А изображается одинаково в натуральную величину и на плоскости П2, и на плоскости П4.
Это обстоятельство позволяет определить положение проекции A4, в системе плоскостей П1 _|_ П4 (рис. 65, б) на комплексном чертеже. Для этого достаточно измерить высоту точки на заменяемой плоско-
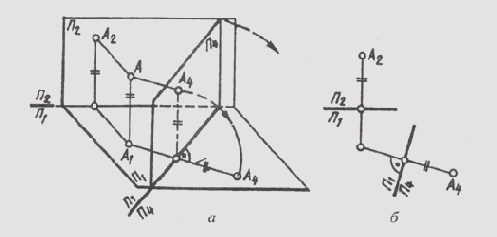
Рис. 65
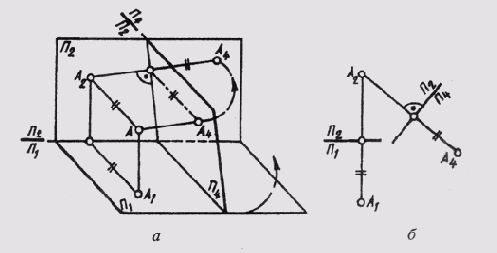
Рис.
66
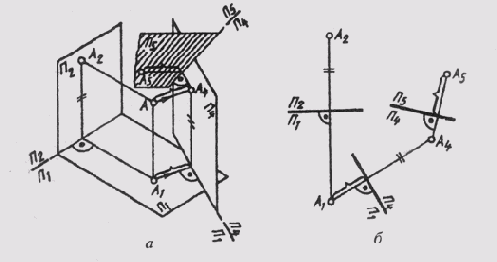
Рис.
67
Если новую плоскость проекций ввести взамен горизонтальной плоскости проекций, т. е. П4 _|_ П2 (рис. 66, а), тогда в новой системе плоскостей новая проекция точки будет находиться на одной линии связи с фронтальной проекцией, причем А2А4 _|_. В этом случае глубина точки одинакова и на плоскости П1, и на плоскости П4. На этом основании строят А4 (рис. 66, б) на линии связи А2А4 на таком расстоянии от новой оси П1/П4 на каком А1 находится от оси П2/П1.
Как уже отмечалось, построение новых дополнительных проекций всегда связано с конкретными задачами. В дальнейшем будет рассмотрен ряд метрических и позиционных задач, решаемых с применением метода замены плоскостей проекций. В задачах, где введение одной дополнительной плоскости не даст желаемого результата, вводят еще одну дополнительную плоскость, которую обозначают П5. Ее располагают перпендикулярно уже введенной плоскости П4 (рис. 67, а), т. е. П5П4 и производят построение, аналогичное ранее рассмотренным. Теперь расстояния измеряют на заменяемой второй из основных плоскостей проекций (на рис. 67, б на плоскости П1) и откладывают их на новой линии связи А4А5, от новой оси проекций П5/П4. В новой системе плоскостей П4П5 получают новый двухпроекционный чертеж, состоящий из ортогональных проекций А4 и А5, связанных линией связи
A4A5_|_П4/П5
§ 37. Прямоугольные координаты точек
Три основные плоскости проекций (П1_|_П2 _|_ П3) могут рассматриваться и как координатные плоскости. Тогда оси проекций становятся координатными осями: осью абсцисс х, П1/П3 —осью координат у,П2/П3 —осью аппликат z.
Начало координат (точка О) располагается в точке пересечения осей координат (рис. 68, а).
Чтобы отнести точку А к натуральной системе координат Oxyz, надо построить ортогональную проекцию точки А на плоскости хОу. Затем проекцию А1 ортогонально проецировать на ось х в точку Ах. Тогда получим пространственную координатную ломаную АА1АХО, отрезки которой параллельны осям координат и соответственно называются: ОАХ — отрезком абсциссы; АХ А1 — отрезком ординат; А1А — отрезком аппликаты.
Измерив координатные отрезки единицей длины l, получим три отвлеченных числа — три координаты точки А:
х = OAX абсцисса; у = AxA1— ордината; z = AA1 — аппликата.
Если точка задана своими координатами А (х, у, z), то можно построить ее комплексный чертеж, задав соответствующую единицу длины l (например, l = 1 мм). Абсцисса точки определяет положение
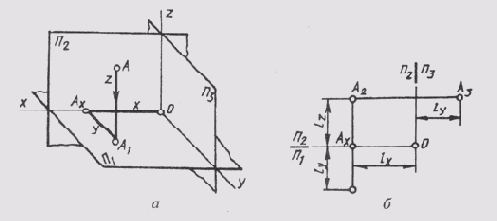
Рис.
68
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Дайте определение комплексного чертежа.
2. Назовите и обозначьте основные плоскости проекций.
3. Что такое вертикальная линия связи, горизонтальная линия связи?
4. Как называется расстояние, определяющее положение точки относительно плоскости проекций П1, П2?
5. Как построить горизонтальную проекцию точки, если на чертеже имеется ее фронтальная, профильная проекции?
6. Как построить фронтальную проекцию точки по данным горизонтальной и профильной проекций точки?
7. Как построить дополнительную проекцию точки на плоскости П4 _|_ П2, П4_|_ П1, П5 _|_ П4?
8. Какие координаты точки можно определить по ее горизонтальной проекции, профильной проекции?
9. Как можно построить комплексный чертеж точки по ее координатам?
