§ 38. Образование линий
В общем случае линию можно представить как множество последовательных положений перемещающейся в пространстве точки. Если точка передвигается без изменения направления, образуется прямая линия, если направление движения точки меняется — образуется кривая линия.
Если точка перемещается в одной плоскости, образуется плоская линия, если ее траектория выходит за пределы одной плоскости — такую линию называют пространственной. Пространственные линии не лежат всеми своими точками в одной плоскости. Их называют также линиями двоякой кривизны.
Примерами плоских линий могут быть окружность, эллипс, овал. В качестве примера пространственной линии можно привести винтовую линию.
Плоские линии делят на циркульные, состоящие из сопряженных дуг окружностей, и лекальные — имеющие переменную кривизну. На чертежах циркульные линии проводятся с помощью циркуля, а лекальные — с помощью лекал.
Графически на чертеже линии задаются с помощью проекций. При этом должна быть показана проекционная связь хотя бы одной ее точки, что позволяет избежать неопределенности.
Простейшим видом линии является прямая.
§ 39. Комплексный чертеж прямой линии
Учитывая то, что прямую линию в пространстве можно определить положением двух ее точек, для построения ее на чертеже достаточно выполнить комплексный чертеж этих двух точек, а затем соединить одноименные проекции точек прямыми линиями. При этом получаем соответственно горизонтальную и фронтальную проекции прямой.
На рис. 69, а показаны прямая l и принадлежащие ей точки А и В. Для построения фронтальной проекции прямой l2 достаточно построить фронтальные проекции точек А2 и В2 и соединить их прямой. Аналогично строится горизонтальная проекция, проходящая через горизонтальные проекции точек А1 и В1. После совмещения плоскости П1 с плоскостью П2 получим двухпроекционный комплексный чертеж прямой l (рис. 69, б).
Профильную проекцию прямой можно построить с помощью профильных проекций точек А и В. Кроме того, профильную проекцию прямой можно построить, используя разность расстояний двух ее точек до фронтальной плоскости проекций, т. е. разность глубин точек (рис. 69, в). В этом случае отпадает необходимость наносить оси проекций на чертеж. Этот способ, как более точный, и используется в практике выполнения технических чертежей.
§ 40. Расположение прямой относительно плоскостей проекций
Относительно плоскостей проекций прямая может занимать различное положение. Прямую, не параллельную ни одной из основных плоскостей проекций (см. рис. 69), называют прямой общего положения. Прямую, параллельную или перпендикулярную одной из плоскостей проекций, называют прямой частного положения.
Прямые, параллельные одной из плоскостей проекций, называют прямыми уровня. Название их зависит от того, какой плоскости они параллельны. Прямую, параллельную горизонтальной плоскости проекций, называют горизонталью и обозначают на чертежах h (рис. 70).
Прямую, параллельную фронтальной плоскости проекций, называют фронталью и обозначают f (рис.71).
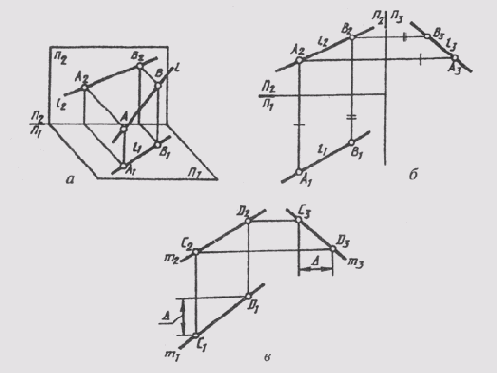
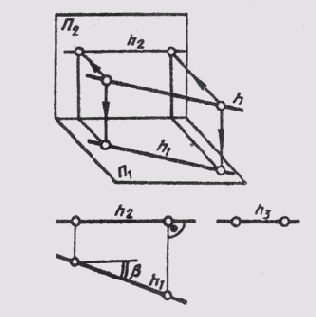
Рис. 70
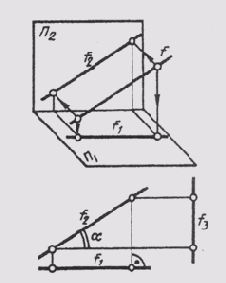
Рис. 71
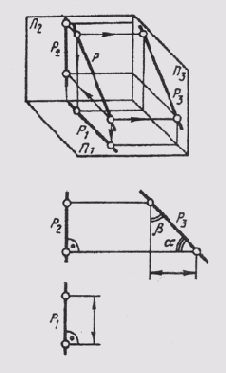
Рис.
72
У прямой уровня одна проекция параллельна самой прямой и определяет углы наклона этой прямой к двум другим плоскостям проекций.
Параллельность одной из плоскостей проекций определяет расположение двух других проекций прямой уровня:
h2 || П2/П1 ;
h3 _|_ П2/П3 ;
f2 || П2/П1;
f3 _|_ П2/П3 ;
p1 _|_ П2/П1 ;
p2 _|_ П2/П1 ;
Прямые h2 и f1 перпендикулярны вертикальным линиям связи; р1 и р2 располагаются на одной вертикальной линии связи и при двухпроекционном чертеже должны быть определены двумя точками прямой р.
Прямые, перпендикулярные одной из плоскостей проекций, называются проецирующими. Эти прямые, будучи перпендикулярными одной плоскости проекций, оказываются параллельными двум другим плоскостям проекций. Поэтому у проецирующих прямых одна проекция превращается в точку, а две другие проекции параллельны самой
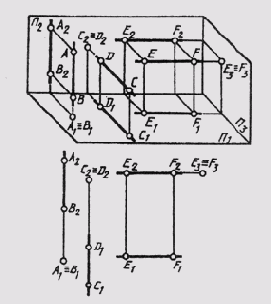
Рис.
73
§ 41. Взаимное расположение двух прямых
Две прямые пространства могут иметь различное расположение (рис. 74). Они могут совпадать а = b, быть параллельными c|| d, пересекаться т ^ n и скрещиваться (k° / l).
Если две прямые параллельны, то на комплексном чертеже (рис. 75, а) их одноименные проекции параллельны.
Если две прямые пересекаются в некоторой точке М, то проекции этой точки должны принадлежать одноименным проекциям прямых, т. е. точки пересечения одноименных проекций пересекающихся прямых должны лежать на одной линии связи (рис. 75, б):
m^n=M->{m1^n1=M1 или m2^n2= М2}
Если две прямые скрещиваются, то их одноименные проекции могут пересекаться в точках, не лежащих на одной линии связи (рис. 75, в):
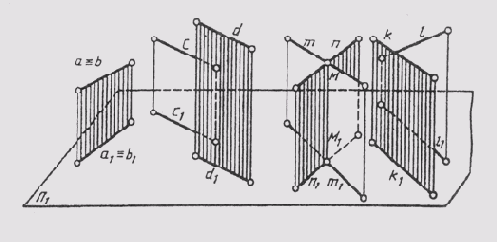
Рис. 74
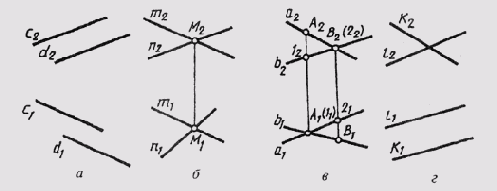
Рис.
75
k0 /l ->{ k2 ^ l2 или k1 || l1}
Следует обратить внимание на особые случаи определения взаимного расположения двух прямых в пространстве. Если одна из них (рис. 76, а) или обе (рис. 76, б) окажутся профильными прямыми, то для определения их взаимного расположения необходимо построить третью, профильную проекцию этих прямых. Если рассматривать рис. 76, а, можно ошибочно сделать предположение, что прямые АВ и CD пересекаются. Однако если построить профильные проекции этих прямых, станет видно, что они скрещиваются, так как точки 1 и 2 не совпадают, а являются фронтально конкурирующими точками.
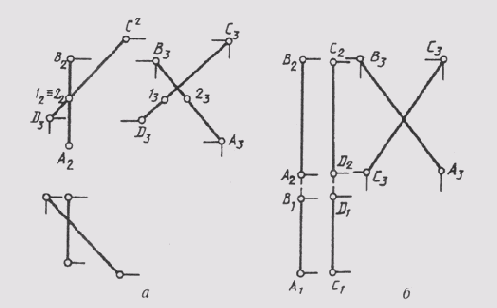
Рис. 76
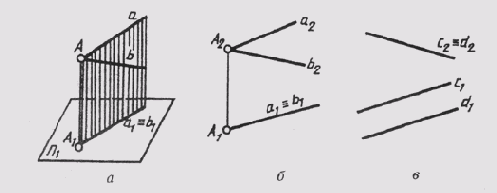
Рис.
77
Две прямые, параллельные или пересекающиеся, могут иметь общую проецирующую плоскость (рис. 77, а). Тогда их изображения на соответствующую плоскость проекций совпадут. Такие прямые называют конкурирующими:
a^b=A->{а2 ^b2=А2 или а1==b1 ,A1~а1(b1)}
Прямые а и b горизонтально конкурирующие, имеют общую горизонтально проецирующую плоскость (рис. 77, б). Прямые с и d (рис. 77, в) — фронтально конкурирующие, имеют общую фронтально проецирующую плоскость.
§ 42. Определение натуральной величины отрезка прямой линии
При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.
Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см. рис. 69).
Возьмем отрезок общего положения АВ (A ^ П1) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А1ВВ1, в котором гипотенузой является сам отрезок, одним катетом — горизонтальная проекция этого отрезка, а вторым катетом — разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.
Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П1.
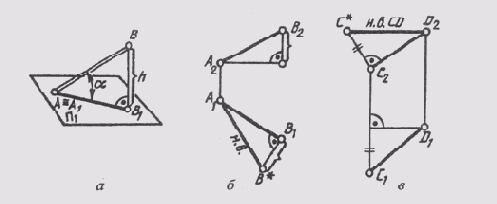
Рис.
78
§ 43. Кривые линии
Кривые линии на комплексном чертеже задают своими проекциями, которые строят по проекциям отдельных точек, принадлежащих этой линии. Проекции линий при ортогональном проецировании получают как результат пересечения проецирующих цилиндров с плоскостями проекций (см. § 28); это означает, что проекциями плоских и пространственных кривых линий являются линии плоские. На рис. 79 видно, что секущая т кривой а в общем случае проецируется секущей ее проекции, а касательная/к кривой проецируется касательной к ее проекции.
На комплексном чертеже кривой ее особые точки, к которым относятся точки перегиба, возврата, излома, узловые точки, являются особыми точками и на ее проекции. Это объясняется тем, что особые точки кривых связаны с касательными в этих точках.
Если плоскость кривой занимает проецирующее положение (рис. 80, а), то одна проекция этой кривой имеет форму прямой. У пространственной кривой все ее проекции — кривые линии (рис. 80, б).
Чтобы установить по чертежу, какая задана кривая (плоская или пространственная), необходимо выяснить, принадлежат ли все точки кривой одной плоскости. Заданная на рис. 80, б кривая является пространственной, так как точка D кривой не принадлежит плоскости, определяемой тремя другими точками А, В и Е этой кривой.
Построение и изображение кривых рассматривалось в § 21,22, поэтому приведем пример изображения на чертеже только окружности как плоской кривой и винтовой линии как пространственной кривой.
Окружность — плоская кривая второго порядка, ортогональная проекция которой может быть окружностью и эллипсом (рис. 81, а). Для изображения окружности диаметра d на комплексном чертеже обязательно строят проекции центра О и двух ее диаметров. Удобнее всего строить проекции диаметров, параллельных плоскостям проекций: АВ || П1 CD || П2; CD _|_ П1 (рис. 81, б). Фронтальная проекция окружности — эллипс — определяется малой осью эллипса A1B2 = dcos b и большой осью эллипса С2D2=d
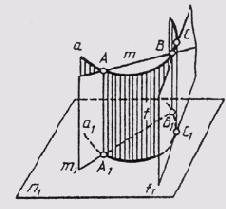
Рис. 79
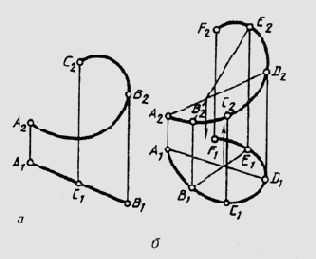
Рис. 80

Рис.
81
Цилиндрическая винтовая линия (гелиса) — пространственная кривая, представляющая собой траекторию точки, выполняющей винтовое движение. Винтовое движение включает в себя равномерное поступательное движение точки по прямой и равномерное вращательное движение этой прямой с точкой вокруг оси i, которой прямая параллельна. Высота p, на которую точка поднимается по прямой за полный оборот, называется шагом винтовой линии (рис. 82). Если ось i винтовой линии перпендикулярна горизонтальной плоскости проекций, то горизонтальная проекция винтовой линии есть окружность, а фронтальная — синусоида.
Для построения фронтальной проекции винтовой линии при заданном диаметре d и шаге р нужно разделить и окружность, и шаг на равное число частей. Построение проекций точки винтовой линии показано на рис. 82. Цилиндрическую винтовую линию можно развер-
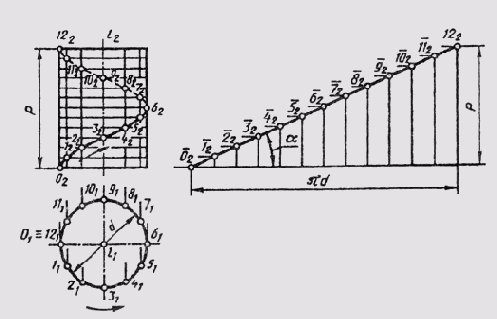
Рис.
82
§ 44. Взаимное расположение точки и линии
Точка в пространстве по отношению к линии может занимать два положения: принадлежать ей или не принадлежать. Если она принадлежит линии, она составляет с ней единое целое и проекции ее на чертеже лежат на соответствующих проекциях линии, а также на одной линии связи.
Если же хотя бы одна из проекций точки не лежит на проекции линии, точка ей не принадлежит. На рис. 83 показан комплексный чертеж линии l, а также ряда точек. Из чертежа видно, что точка А принадлежит линии b, так как горизонтальная ее проекция А1 лежит на горизонтальной проекции линии 11, а фронтальная проекция точки А2 расположена на фронтальной проекции прямой А и ле-
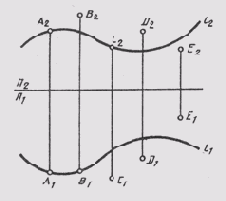
Рис.
83
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ
1. Дайте определение линии.
2. Чем отличается плоская линия от пространственной?
3. Приведите примеры, плоских и пространственных линий.
4. Чем отличается образование прямой линии от кривой?
5. Чем определяется проекция прямой линии?
6. Какое положение может занимать прямая относительно плоскостей проекций?
7. Какие линии относятся к линиям уровня? Какие линии уровня вы знаете?
8. Какие линии относятся к проецирующим? Назовите виды проецирующих линий.
9. Как определить истинную величину отрезка по его комплексному чертежу?
10. Как могут быть расположены в пространстве две прямые линии?
11. Как изображается окружность на комплексном чертеже, если она лежит во фронтально проецирующей плоскости; во фронтальной плоскости уровня; в плоскости общего положения?
12. Как можно построить эллипс — прямоугольную проекцию окружности, расположенной во фронтально проецирующей плоскости?
13. Какие параметры определяют цилиндрическую винтовую линию?
